Ein Algorithmus zum Layoutproblem

Ein Algorithmus zur Ermittlung einer suboptimalen Lösung für das Layoutproblem durch Berechnung und Auswertung der Kostendifferentialquotienten

Das Layoutproblem (auch innerbetriebliches Standortproblem genannt) läßt sich folgendermaßen beschreiben: Eine Anzahl von o Anordnungsobjekten soll auf O Standorte platziert werden, so daß die Gesamttransportkosten möglichst minimal werden. Die Transportmengen zwischen den Anordnungsobjekten und die Entfernungen zwischen den Standorten sind bekannt. Die Kosten werden als proportional zur Menge und Entfernung angenommen.
Der hier vorgestellte Algorithmus ist ein Eröffnungsverfahren, d. h. es wird eine zulässige Ausgangslösung erzeugt, auf die nachfolgend ein Verbesserungsverfahren angewandt werden kann. Das Layoutproblem gilt als NP-schweres Problem, d. h. es ist bis heute kein Verfahren bekannt, mit welchem man immer mit polynomialem Aufwand eine optimale Lösung ermitteln kann. Es ist deshalb wichtig, daß ein Eröffnungsverfahren möglichst schon eine gute Lösung liefert, da einige herkömmliche Verbesserungsverfahren (z.B. Zweier-Austauschverfahren) diese Lösung nur bis zum nächsten lokalen Minimum verbessern. Das hier vorgestellte Eröffnungsverfahren liefert stets eine Lösung, die nie schlechter, in der Regel wesentlich besser als der Mittelwert aller möglichen Lösungen ist.

Mathematisches Modell

gegeben:
	o	Anzahl der Objekte
	O	Anzahl der Orte ( O = o )
	m_ij	Menge, die von Objekt i nach Objekt j zu transportieren ist
	S_kl	Entfernung von Ort k nach Ort l
gesucht:
	u_ik	ist 1 wenn Objekt i am Ort k platziert wird, sonst 0
	s_ij	Entfernung von Objekt i nach Objekt j
	M_kl	Menge, die von Ort k nach Ort l zu transportieren ist

Nebenbedingungen:

Zielfunktion:

Die Mengen, die von Objekt i nach Objekt i zu tranportieren sind und die Entfernung vom Ort k zum Ort k sind jeweils Null, d. h. die Matrizen der m- und der S-Werte müssen auf ihren Diagonalen jeweils mit Nullen belegt sein alle anderen Werte müssen größer oder gleich Null sein. Das ist für den hier vorgestellten Algorithmus von Bedeutung. Statt der sonst üblichen Bezeichnung für die Entfernung mit d (Distance) wird hier der Buchstabe s bzw. S verwendet, da das Symbol d für die Differentiale benötigt wird.

1 Berechnung der Gleichgewichtslösung

Es werden reelle Zuordnungsvariable x_ik eingeführt, die im Bereich [ 0, 1 ] jeden Wert annehmen können. Die Anzahl der noch nicht zugeordneten Objekte und Orte sei Q. Wenn ein Objekt m zu einem Ort n bereits zugeordnet wurde, so sei u_mn gleich 1 und alle anderen u_in und u_mk gleich 0, sonst sei u_mn gleich -1.
Die x_mn der Gleichgewichtslösung sind dann zu berechnen durch:

Dadurch werden bis auf die Ganzzahligkeitsbedingung der Zuordnungsvariablen alle anderen Nebenbedingungen erfüllt.

2 Berechnung der Differentiale der reellen Zuordnungsvariablen

Es wird für alle i und k untersucht, wie sich eine differentielle Änderung der reellen Zuordnungsvariable x_ik um dx_ik bei der Gleichgewichtslösung auf die differentielle Änderung der Gesamttransportkosten auswirkt. Eine primäre differentielle Änderung einer reellen Zuordnungsvariable muß dabei durch die sekundäre differentielle Änderung aller anderen Zuordnungsvariablen kompensiert werden, so daß die differentiell veränderte Gleichgewichtslösung eine hinsichtlich der Nebenbedingungen zulässige Lösung bleibt (siehe Abbildung).

Die primäre differentielle Änderung einer reellen Zuordnungsvariable kann dabei rückwärts aus den sekundären differentiellen Änderung aller anderen reellen Zuordnungsvariablen berechnet werden.
Bei einer primären differentiellen Änderung der reellen Zuordnungsvariable x_ik um dx_ik lassen sich damit die sekundären differentiellen Änderungen der reellen Zuordnungsvariablen folgendermaßen berechnen:

Für die primäre differentielle Änderung der reellen Zuordnungsvariable x_ik um dx_ik erhält man:

3 Berechnung der Matrix der Kostendifferentialquotienten

Für die Kostendifferentialquotienten K'_ik erhält man:

Falls u_ik > -1:

Falls u_ik = -1:

Mit

erhält man nach Ausführung der Differentiation:

Weitere Umformungen ergeben:

Für die Auswertung kann der reduzierte Kostendifferentialquotient K'_ij^red verwendet wurden. (Da der erste Term in K'_ij konstant ist und damit keinen Beitrag liefert, kann er weggelassen werden, anschließend kann zusätzlich der konstante Faktor Q weggelassen werden.)

4 Grundform des Algorithmus zur Ermittlung einer Lösung

1. Startwertinitialisierung:

Q = o = O

2. Solange Q > 1:

Berechnung aller x_mn der Gleichgewichtslösung:

Falls u_mn < 0: x_mn = 1/Q, sonst x_mn = u_mn
Berechnung der Hilfsgrößen:
Berechnung der Matrix der reduzierten Kostendifferentialquotienten:
Aufsuchen von i und k, so daß K'_ik^red minimal wird
alle u_inund u_mk gleich 0 setzen, u_ik gleich 1 setzen
Q um 1 verringern

3. Berechnung der Transportmengen und -entfernungen und des Zielfunktionswertes:

u_ik aufsuchen, welches gleich -1 ist (genau eine Variable) und gleich 1 setzen
Berechnung aller s_ij und M_kl durch die Gleichungen der Nebenbedingungen
Berechnung des Zielfunktionswertes

5 Erweiterung des Algorithmus

Der Algorithmus leitet aus bestehenden (relativen) Unterschieden bei den Entfernungen zwischen den Orten und den Transportmengen zwischen den Objekten eine Entscheidung ab, welches Objekt als nächstes welchem Ort zugeordnet werden sollte. Es läßt sich zeigen, daß eine optimale Zuordnung eines beliebigen Layout-Problems auch eine optimale Zuordnung des Problems ist, bei dem gegenüber dem ersten alle Entfernungen um einen beliebigen (aber konstanten) Wert geändert wurden, dabei können die Entfernungen auch negativ werden (sofern alle Mengen nichtnegativ sind). Bei diesem Algorithmus ist es sinnvoll, statt der Werte der Entfernungen S_kl die um den Mittelwert aller Entfernungen reduzierten Werte S_kl - S^quer bei der Berechnung zu verwenden. Dadurch werden die relativen Unterschiede vergrößert und der Algorithmus ermittelt in der Regel eine bessere Lösung.
Eine weitere Möglichkeit besteht in der Gewichtung der K'^red-Werte durch die Transportmengen vor der Auswahl des kleinsten (negativsten) Wertes. Dadurch kann verhindert werden, daß bereits zum Beginn die "besten" Orte durch Objekte verbraucht werden, die nur geringe Transportmengen aufweisen. Es muß dabei jedoch beachtet werden,daß die K'^red-Werte gegenüber den ursprünglichen K'-Werten verschoben sind, d. h. bei Verwendung gewichteter K'^red-Werte würde man in der Regel eine andere Lösung erhalten, als bei Verwendung der gewichteten K'-Werte. Zu einem Ausweg und gleichzeitig einer sinnvollen Erweiterung gelangt man, indem man die K'^red-Werte um einen Offset verschiebt, so daß der minimale K'^red-Wert kleiner als Null und der maximale K'^red-Wert größer als Null ist. Es kann dann durch die Gewichtung nur ein solches Element zum kleinsten (negativsten) werden, welches bereits vorher negativ war. Zum erweiterten Algorithmus gelangt man somit, indem man

an Stelle des kleinsten K'_ik^red - Wertes

den kleinsten Wert von g_i · (K'_ik^red - K^offset )

verwendet. Gewichte und Offset lassen sich dabei durch die Gleichungen

g_i = ( m_i1 + ... + m_io + m_1i + ... + m_oi )^a

( mit a als frei wählbarem nichtnegativem reellen Parameter ) und

K^offset = Min { K'_ik^red } + b · ( Max { K'_ik^red } - Min { K'_ik^red } )

( mit b als frei wählbarem reelen Parameter aus dem Intervall [ 0..1 ] ) berechnen.

Durch die Verwendung verschiedener Parameterkombinationen können Lösungen erzeugt werden, die im Zielfunktionswert ähnlich gut sind, aber grundsätzlich unterschiedliche Zuordnungen der Anordnungsobjekte zu den Orten aufweisen.
Eine weitere Erweiterung kann darin bestehen, diesen Algorithmus mit einer Monte-Carlo-Methode zu kombinieren, wobei viele Lösungen erzeugt werden, bei denen jeweils eine Parameterkombination auf jedem der O=o Subschritte des Algorithmus zufällig neu erzeugt wird. Gegenüber der herkömmlichen Monte-Carlo-Methode würden damit von vornherein schlechte Lösungen ausgeschlossen werden, wodurch sich ab einer bestimmten Problemgröße der erhöhte Rechenaufwand lohnt.

6 Beispiel

Die Ermittlung der Lösung erfolgt durch den Algorithmus in der Grundform.
Lage der potentiellen Standorte:

1--------2---------------3
 \       |              /
  \      |            /
   \     |          /
    \    |        /
     \   |      /
      \  |    /
       \ |  /
        \|/
         4

Gegebene Daten:

Matrix der S_kl - Werte:

Matrix der m_ij - Werte:

k \ l	1	2	3	4
1	0	9	25	15
2	9	0	16	12
3	25	16	0	20
4	15	12	20	0

i \ j	1	2	3	4
1	0	1	2	5
2	1	0	1	0
3	3	1	0	1
4	4	0	2	0

Ermittlung der Zuordnungsvariablen:

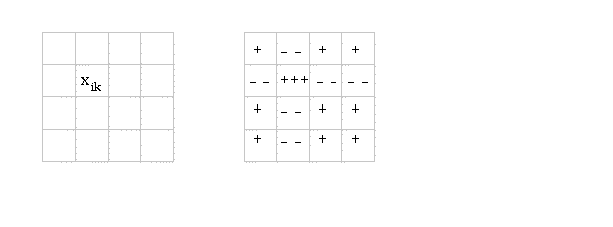
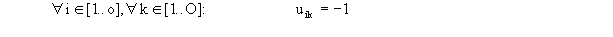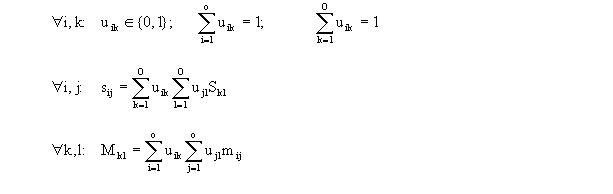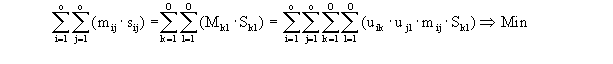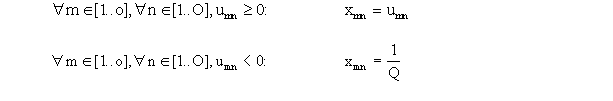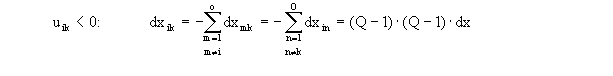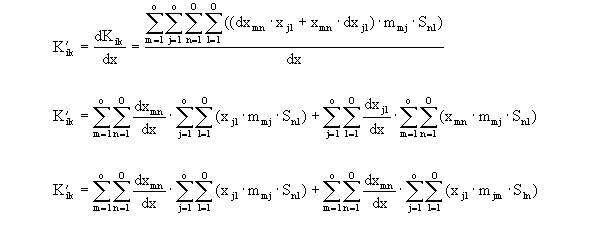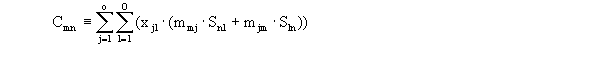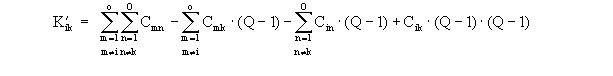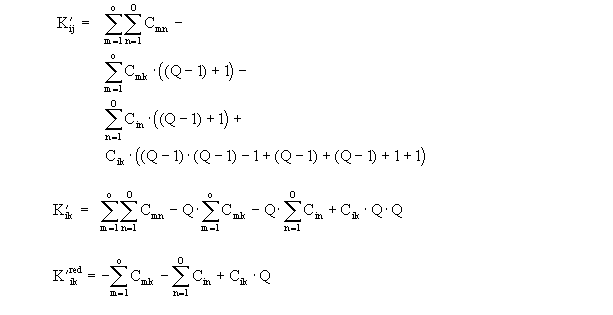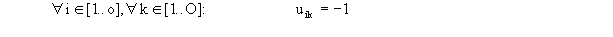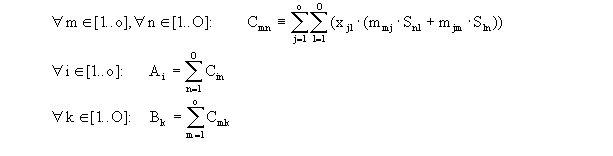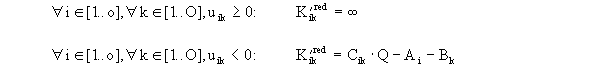Matrix der x_mn - Werte:

Matrix der C_mn - Werte:

Matrix der K'_ik - Werte:

m\n	1	2	3	4
1	0,25	0,25	0,25	0,25
2	0,25	0,25	0,25	0,25
3	0,25	0,25	0,25	0,25
4	0,25	0,25	0,25	0,25

m\n	1	2	3	4
1	196,0	148,0	244,0	188,0
2	49,0	37,0	61,0	47,0
3	122,5	92,5	152,5	117,5
4	147,0	111,0	183,0	141,0

i\k	1	2	3	4	A_i
1	-506,5	-572,5	-440,5	-517,5	776,0
2	-512,5	-434,5	-590,5	-499,5	194,0
3	-509,5	-503,5	-515,5	-508,5	485,0
4	-508,5	-526,5	-490,5	-511,5	582,0
B_k	514,5	388,5	640,5	493,5	-

m\n	1	2	3	4
1	0,33	0,33	0,00	0,33
2	0,00	0,00	1,00	0,00
3	0,33	0,33	0,00	0,33
4	0,33	0,33	0,00	0,33

m\n	1	2	3	4
1	162,0	130,0	284,7	166,0
2	32,0	28,0	81,3	36,0
3	114,0	88,0	162,7	112,0
4	96,0	84,0	244,0	108,0

i\k	1	2	3	4	A_i
1	-660,7	-682,7	9999,9	-666,7	742,7
2	9999,9	9999,9	9999,9	9999,9	177,3
3	-538,7	-542,7	9999,9	-562,7	476,7
4	-648,0	-610,0	9999,9	-630,0	532,0
B_k	404,0	330,0	772,7	422,0	-

m\n	1	2	3	4
1	0,00	1,00	0,00	0,00
2	0,00	0,00	1,00	0,00
3	0,50	0,00	0,00	0,50
4	0,50	0,00	0,00	0,50

m\n	1	2	3	4
1	155,0	179,0	315,0	145,0
2	33,0	21,0	77,0	39,0
3	117,5	63,5	147,5	122,5
4	103,5	31,5	211,5	130,5

i\k	1	2	3	4	A_i
1	9999,9	9999,9	9999,9	9999,9	794,0
2	9999,9	9999,9	9999,9	9999,9	170,0
3	-625,0	9999,9	9999,9	-643,0	451,0
4	-679,0	9999,9	9999,9	-653,0	477,0
B_k	409,0	295,0	751,0	437,0	-

=> x₄₁ = 1 => x₃₄ = 1

Zuordnung der Anordnungsobjekte zu den Standorten:

4        1               2
1--------2---------------3
 \       |              /
  \      |            /
   \     |          /
    \    |        /
     \   |      /
      \  |    /
       \ |  /
        \|/
         4 3

Matrix der u_ik - Werte:

Matrix der s_ij - Werte:

Matrix der m_ij - Werte:

i \ k	1	2	3	4
1	0	1	0	0
2	0	0	1	0
3	0	0	0	1
4	1	0	0	0

i \ j	1	2	3	4
1	0	16	12	9
2	16	0	20	25
3	12	20	0	15
4	9	25	15	0

i \ j	1	2	3	4
1	0	1	2	5
2	1	0	1	0
3	3	1	0	1
4	4	0	2	0

Gesamtkosten:

K =	16 · 1 + 12 · 2 + 9 · 5 +
	16 · 1 + 20 · 1 + 25 · 0 +
	12 · 3 + 20 · 1 + 15 · 1 +
	9 · 4 + 25 · 0 + 15 · 2 = 258

Für dieses kleine Beispiel wurde damit sofort die optimale Lösung gefunden. Bei kleinen Problemen wie diesem (mit 4!=24 Möglichkeiten), kann eine optimale Lösung auch leicht durch Vollenumeration ermittelt werden.

(c) Lutz Tautenhahn 1997, 1999