A Dynamic Programming Algorithm for Single-Item Capacitated Economic Lot Sizing with Start-up Costs, Piecewise Linear Production Costs and Piecewise Linear Holding Costs
Lutz Tautenhahn (1997, 1999, 2001, 2024)
C++ Sourcecode is available at http://www.lutanho.net/plt/lotsize.zip
Online-Version (HTML/JS-Sourcecode) is available at http://www.lutanho.net/plt/lotsize.html (2024)

Contents

1 The general linear integer single-item lot sizing problem
   1. 1 Problem description
   1. 2 Mathematical model
2 Declaration of the required objects and sets
   2. 1 The object field
   2. 2 The field-set
3 Declaration of the required operations
   3. 1 Production-Transformation
   3. 2 Minimum-Interference
   3. 3 Left-Interference
   3. 4 Right-Interference
   3. 5 Section
   3. 6 Consolidation
   3. 7 Holding-Transformation
   3. 8 Optimum-Transformation
4 Definition of the basic operations
   4. 1 Production-Transformation
   4. 2 Minimum-Interference
   4. 3 Left-Interference
   4. 4 Right-Interference
   4. 5 Section
   4. 6 Consolidation
   4. 7 Holding-Transformation
5 Realization of the algorithm to obtain an optimum solution
   5. 1 The domain of feasible solutions
   5. 2 The algorithm for models with no start-up costs
   5. 3 The algorithm for models with start-up costs
6 Appendix
   6. 1 Graphical representation of the algorithm
   6. 2 Computational results

1 The general linear integer single-item lot sizing problem

1. 1 Problem description

 A single product has to be produced over several periods to satisfy the demand, which is know for every period. If the production exceeds the demand, then the product is stored (without any loss) and is used to satisfy the demand of subsequent periods. Production costs and holding costs are piecewise linear functions (not necessarily continuous). Backlogging can be introduced by allowing negative inventory levels with positive holding costs. There are additional start-up costs, which only occur, if the production device runs in the current period and did not run in the previous period. In order to prevent start-up costs, it is possible to keep the production device running in periods with no production, however, there are additional fix production costs in such periods.

1. 2 Mathematical model

 The objective of the optimization is:


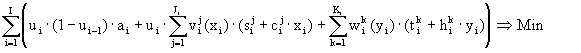
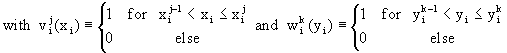
Data:
I- number of periods
ximin- min. feassible production quantity in period i(i = 1...I)
ximax- max. feassible production quantity in period i(i = 1...I)
yimin- min. feassible inventory quantity in period i(i = 1...I-1)
yimax- max. feassible inventory quantity in period i(i = 1...I-1)
y0- inventory quantity at the end of period 0
yI- inventory quantity at the end of period I
Ji- number of production intervals in period i(i = 1...I)
Ki- number of inventory intervals in period i(i = 1...I)
xij- upper border of production interval j in period i(i = 1...I, j = 0...Ji)
yik- upper border of inventory interval k in period i(i = 1...I, k = 0...Ki)
ai- start-up costs in period i(i = 1...I)
sij- fix production costs in period i in interval j(i = 1...I, j = 1...Ji)
cij- variable production costs in period i in interval j(i = 1...I, j = 1...Ji)
tik- fix inventory costs in period i in interval k(i = 1...I, k = 1...Ki)
hik- variable inventory costs in period i in interval k(i = 1...I, k = 1...Ki)
di- demand in period i(i = 1...I)
u0- binary production variable in period 0
Variables:
ui- binary production variable in period i(i = 1...I)
xi- production quantity in period i(i = 1...I)
yi- inventory quantity at the end of period i(i = 1...I -1)

Restrictions for the binary production variable:

Restrictions for the borders of the production intervals:

Restrictions for the production quantity:

Restrictions for the borders of the inventory intervals:

Restrictions for the inventory quantity:

Balance of inventory quantity:


2 Declaration of the required objects and sets

2. 1 The object field

A field is an object with the following 6 properties:
pl(integer)predecessor left
pr(integer)predecessor right
le(integer)left
ri(integer)right
hl(integer)height left
dh(integer)derivative of height

A field is an invalid field (no field) if:
ri < le or
hl < 0 or
hl + (ri-le) * dh < 0
In order to operate with the property * of a field f, the notation f .* is used (f .pl, f.pr, ...).
In this way a field can represent a piece of a piecewise linear total cost function or a piece of any other piecewise linear function.

2. 2 The field-set

A field-set Fn (in the following also simply called set) consists of n distinct fields:
Fn = {f1, ..., fn}
A set Fn is sorted, if and only if:
fi.le < fi+1.le + 1or(for all i = 1...n-1)(left sorted)
fi.ri < fi+1.ri + 1or(for all i = 1...n-1)(right sorted)
( fi.le< fi+1.le + 1 and fi.ri< fi+1.ri + 1 )(for all i = 1...n-1)(both side sorted)

A set Fn is well-formed , if and only if:
fi.ri + 1 = fi+1.le (for all i = 1...n-1)
In this way a well-formed field-set can represent a piecewise linear total cost function or any other piecewise linear function.

3 Declaration of the required operations

3. 1 Production-Transformation

 3. 1. 1 Production-Transformation of a field f by a field d

The result of a Production-Transformation p* (* = d0, dl, dr, fl, fr) of a field f by a field d is the set F*1 = {f*1}. The calculation instruction is given in chapter 4.

In general:
F*1 = p*(f, d)
Meaning:
pd0production quantity = 0 for an entire inventory interval; without set-up costs; no start-up costs in this period; start-up costs in the next period possible
pdlproduction quantity = left border of the production interval for an entire inventory interval; with set-up costs; start-up costs in this period possible, in the next period impossible
pdrproduction quantity = right border of the production interval for an entire inventory interval; with set-up costs; start-up costs in this period possible, in the next period impossible
pflinventory quantity = left border of the inventory interval for an entire production interval; with set-up costs; start-up costs in this period possible, in the next period impossible
pflinventory quantity = right border of the inventory interval for an entire production interval; with set-up costs; start-up costs in this period possible, in the next period impossible

3. 1. 2 Production-Transformation of a field-set Fn by a field d

The result of a Production-Transformation P* (* = d0, dl, dr, fl, fr) of a set Fn by a field d is the set F*n. If the set Fn is well-formed then the resulting sets Fd0n, Fdln and Fdrn are well-formed, Ffln and Ffrn are both side sorted.

In general:
F*n = { f*1, ..., f*n }= P* (Fn, d) = { p* ( f1 , d), ..., p* ( fn , d) }
Meaning:
If Fn is the representation of a total cost function in a certain period and d is the representation of the appropriate production cost function (linear plus set-up costs) in this period then the resulting field-sets include the representation of all possible extremal production transformations. So the optimum production transformation can be represented by at least one of these resulting field-sets for each inventory level.

3. 2 Minimum-Interference

3. 2. 1 Minimum-Interference of a field f with a field d

The result of a Minimum-Interference m of a field f with a field d is a set F1 = { f1 }, a set G2 = {g1, g2} or a set H3 = {h1, h2, h3}, respectively.
The order of f and d may not be exchanged. The resulting set is always well-formed. The calculation instruction is given in chapter 4.

In general:
Fmk = m(f, d) (k = 1, 2 or 3)
Meaning:
If f is the representation of a possible total cost function in the interval [f.le, f.ri] and d is the representation of another possible total cost function in the interval [d.le, d.ri] then the resulting field-set is the representation of the minimum total costs of both in the interval [f.le, f.ri].
3. 2. 2 Minimum-Interference of a well-formed field-set Fn with a field g

The result of a Minimum-Interference M of a well-formed set Fn = {f1, ..., fn} with a field g is the well-formed set FMk = {m(f1, g), ..., m(fn, g)}.

In general:
FMk = {m(f1, g), ..., m(fn, g)} = M ( Fn , g) = M ({f1, ..., fn}, g) (k>n-1)
Meaning:
If Fn is the representation of a possible total cost function in the interval [f1.le, fn.ri] and d is the representation of another possible total cost function in the interval [d.le, d.ri] then the resulting field-set is the representation of the minimum total costs of both in the interval [f1.le, fn.ri].
3. 2. 3 Minimum-Interference of a well-formed field-set Fn with a (not necessarily sorted) field-set Go

The result of a Minimum-Interference MM of a well-formed set Fn = {f1, ..., fn} with a set Go is the well-formed set FMMk . The set has to be calculated recursively by
F1n(1) = M (Fn ,g1)
and
Fi+1n(i+1) = M (Fin(i) ,gi+1) for i = 1...o-1
In general:
FMMk = MM (Fn ,Go) = Fon(o) (k>n-1)
Meaning:
If Fn is the representation of a possible total cost function in the interval [f1.le, fn.ri] and Go is the representation of o other possible total cost functions in the intervals [g1.le, g1.ri], ..., [go.le, go.ri] then the resulting field-set is the representation of the minimum total costs of all in the interval [f1.le, fn.ri].

3. 3 Left-Interference

 3. 3. 1 Left-Interference of a field f with a field d

The result of a Left-Interference l of a field f with a field d is the set Flk = { fl1 , ..., flk }. The order of f and d may not be exchanged. The resulting set is always well-formed. The calculation instruction is given in chapter 4.

In general:
Flk = l(f, d) (k = 1, 2, 3 or 4)
Meaning:
If f is the representation of a possible total cost function in the interval [f.le, f.ri] and d is the representation of another possible total cost function in the interval [d.le, d.ri] and f.le-2<d.ri holds then the resulting field-set is the representation of the minimum total costs of both in the interval [Min{f.le, d.le}, f.ri] else in the interval [f.le, f.ri].
3. 3. 2 Left-Interference of a well-formed field-set Fn with a field g

The result of a Left-Interference L of a well-formed set Fn = {f1, ..., fn} with a field g is the well-formed set FLk = {l(f1, g), m(f2, g), ..., m(fn, g)}.

In general:
FLk = { l(f1, g), m(f2, g), ..., m(fn, g)} = L ( Fn , g) = L ({f1, ..., fn}, g) (k>n-1)
Meaning:
If Fn is the representation of a possible total cost function in the interval [f1.le, fn.ri] and d is the representation of another possible total cost function in the interval [d.le, d.ri] and f1.le-2<d.ri holds then the resulting field-set is the representation of the minimum total costs of both in the interval [Min{ f1.le, d.le}, fn.ri] else in the interval [f1.le, fn.ri].
3. 3. 3 Left-Interference of a well-formed field-set Fn with a sorted field-set Go

The result of a Left-Interference LL of a well-formed set Fn = {f1, ..., fn} with a sorted set Go is the well-formed set FLLk . The set has to be calculated recursively by
F1n(1) = L (Fn ,go)
and
Fi+1n(i+1) = L (Fin(i) ,go-i) for i = 1...o-1
In general:
FLLk = LL (Fn ,Go) = Fon(o) (k>n-1)
Meaning:
If Fn is the representation of a possible total cost function in the interval [f1.le, fn.ri] and Go is the representation of o other possible total cost function in o intervals on [g1.le, go.ri] and f1.le-2< go.ri holds then the resulting field-set is the representation of the minimum total costs of all in the interval [Min{ f1.le, g1.le}, fn.ri] else in the interval [f1.le, fn.ri].

3. 4 Right-Interference

 3. 4. 1 Right-Interference of a field f with a field d

The result of a Right-Interference r of a field f with a field d is the set Frk = { fr1 , ..., frk }. The order of f and d may not be exchanged. The resulting set is always well-formed. The calculation instruction is given in chapter 4.

In general:
Frk = r(f, d) (k = 1, 2, 3 or 4)
Meaning:
If f is the representation of a possible total cost function in the interval [f.le, f.ri] and d is the representation of another possible total cost function in the interval [d.le, d.ri] and f.ri+2>d.le holds then the resulting field-set is the representation of the minimum total costs of both in the interval [f.le, Max{f.ri, d.ri}] else in the interval [f.le, f.ri].
3. 4. 2 Right-Interference of a well-formed field-set Fn with a field g

The result of a Right-Interference R of a well-formed set Fn = {f1, ..., fn} with a field g is the well-formed set FRk = {m(f1, g), ..., m(fn-1, g), r(fn, g)}.

In general:
FRk = {m(f1, g), ..., m(fn-1, g) ), r(fn, g)} = R ( Fn , g) = R ({f1, ..., fn}, g) (k>n-1)
Meaning:
If Fn is the representation of a possible total cost function in the interval [f1.le, fn.ri] and d is the representation of another possible total cost function in the interval [d.le, d.ri] and fn.ri+2>d.le holds then the resulting field-set is the representation of the minimum total costs of both in the interval [ f1.le, Max{fn.ri, d.ri}] else in the interval [f1.le, fn.ri].
3. 4. 3 Right-Interference of a well-formed field-set Fn with a sorted field-set Go

The result of a Right-Interference RR of a well-formed set Fn = {f1, ..., fn} with a sorted set Go is the well-formed set FRRk . The set has to be calculated recursively by
F1n(1) = R (Fn ,g1)
and
Fi+1n(i+1) = R (Fin(i) ,gi+1) for i = 1...o-1
In general:
FRRk = RR (Fn ,Go) = Fon(o) (k>n-1)
Meaning:
If Fn is the representation of a possible total cost function in the interval [f1.le, fn.ri] and Go is the representation of o other possible total cost function in o intervals on [g1.le, go.ri] and fn.ri+2> g1.le holds then the resulting field-set is the representation of the minimum total costs of all in the interval [f1.le, Max{fn.ri, gn.ri}] else in the interval [f1.le, fn.ri].

3. 5 Section

 3. 5. 1 Section of the field f on the interval [Inf, Sup]

The result of a Section s of a field f on the interval [Inf, Sup] is an empty field-set Fs0 = {} or the set Fs1 = {fs1}. The calculation instruction is given in chapter 4.

In general:
Fsk = s (f, Inf, Sup) (k = 0 or 1)
Meaning:
If f is the representation of a possible total cost function in the interval [f.le, f.ri] then the resulting field-set is the representation in the interval [Max{ f.le, Inf}, Min{f.ri, Sup}].
3. 5. 2 Section of a well-formed field-set Fn on the interval [Inf, Sup]

The result of a Section S of a well-formed set Fn = {f1, ..., fInf, ..., fSup, ..., fn} on the interval [Inf, Sup] is the well-formed set FSk.
In general:
FSk= S (Fn, Inf, Sup)
= {s(f1, Inf, Sup), ..., s(fInf, Inf, Sup), ..., s(fSup, Inf , Sup), ..., s(fn, Inf, Sup)}
= {s(fInf, Inf, Sup), ..., s(fSup, Inf, Sup)}
= {s(fInf, Inf, Sup), fInf+1, ..., fSup-1, s(fSup, Inf, Sup)}
= {fS1, ..., fSk} (k<n+1)
Meaning:
If Fn is the representation of a possible total cost function in the interval [f1.le, fn.ri] then the resulting field-set is the representation in the interval [Max{ f1.le, Inf}, Min{fn.ri, Sup}].

3. 6 Consolidation

 3. 6. 1 Consolidation of a field f1 with a field f2

The result of a Consolidation c of a field f1 with a field f2 is the set Fc2 = {f1 , f2} or the set Gc1 = {g1}. The calculation instruction is given in chapter 4.

In general:
Fck = c (f1, f2) (k = 1 or 2)
Meaning:
If f1 is the representation of a possible total cost function in the interval [f1.le, f1.ri] and f2 is the representation of another possible total cost function in the interval [f2.le, f2.ri] and f1.ri+1=f2.le holds and the two fields can be consolidated (i.e. the fields ‘fit’ together) then the resulting field-set consists of only one field that is the representation of both in the interval [f1.le, f2.ri] else the resulting field-set consists of the two fields f1 and f2. In this way it is possible to reduce data without any loss of information.
3. 6. 2 Consolidation of a well-formed field-set Fn at position i

The result of a Consolidation C of a well-formed set Fn = {f1, ..., fn} at position i is the well-formed set FCk.

In general:
FCk = C (Fn, i) = {f1, ..., c(fi, fi+1), ..., fn} (k = n-1 or n)
Meaning:
If Fn is the representation of a possible total cost function then the resulting field-set is the representation of the same cost function with a Consolidation of the fields fi and fi+1. In this way it is possible to reduce data without any loss of information.
3. 6. 3 Total Consolidation of a well-formed field-set Fn

The result of a total Consolidation CC of a well-formed set Fn = {f1, ..., fn} is the well-formed set FCCk. The set has to be calculated recursively by
F1n(1) = C (Fn, n-1)
and
Fi+1n(i+1) = C (Fn(i), n-(i+1)) for i = 1 ... n-2
In general:
FCCk = CC (Fn) = Fn-1n(n-1) (k<n+1)
Meaning:
If Fn is the representation of a possible total cost function then the resulting field-set is the representation of the same cost function with a minimum number of fields. In this way it is possible to reduce data without any loss of information.

3. 7 Holding-Transformation

 3. 7. 1 Linear Holding-Transformation of a field f by a field g

The result of a Linear Holding-Transformation h of a field f by a field g is the field-set Fhk. The calculation instruction is given in chapter 4.

In general:
Fhk = h (f, g) (k = 1, 2 or 3)
Meaning:
If f is the representation of a total cost function without holding costs in the interval [f.le, f.ri] and g is the representation of a linear holding cost function in the interval [g.le, g.ri] then the resulting field-set is the representation of the same total cost function in the interval [f.le, f.ri] with additional holding costs in the interval [g.le, g.ri].
3. 7. 2 Linear Holding-Transformation of a well-formed field-set Fn by a field g

The result of a Linear Holding-Transformation H of a well-formed set Fn = {f1, ..., fn} by a field g is the well-formed set FHk.

In general:
FHk = H (Fn, g) = {h(f1, g), ..., h(fn, g)}= {fH1, ..., fHk} (n-1<k<n+3)
Meaning:
If Fn is the representation of a total cost function without holding costs in the interval [f1.le, fn.ri] and g is the representation of a linear holding cost function in the interval [g.le, g.ri] then the resulting field-set is the representation of the same total cost function in the interval interval [f1.le, fn.ri] with additional holding costs in the interval [g.le, g.ri].
3. 7. 3 Piecewise Linear Holding-Transformation of a well-formed field-set Fn by a well-formed field-set Go

The result of a Piecewise Linear Holding-Transformation HH of a well-formed set Fn = {f1, ..., fn} by a well-formed set Go is the well-formed set FHHk . The set has to be calculated recursively by
F1n(1) = H (Fn ,g1)
and
Fi+1n(i+1) = H (Fin(i) ,gi+1) for i = 1...o-1
In general:
FHHk = HH (Fn ,Go) = Fon(o) (k>n-1)
Meaning:
If Fn is the representation of a total cost function without holding costs in the interval [f1.le, fn.ri] and Go is the representation of a piecewise linear holding cost function in the interval [g1.le, go.ri] then the resulting field-set is the representation of the same total cost function in the interval [f1.le, fn.ri] with additional holding costs in the interval [g1.le, go.ri].

3. 8 Optimum-Transformation

 3. 8. 1 Optimum-Transformation op of a well-formed field-set Fn by a field d on an interval [Inf, Sup]

The result of an Optimum-Transformation op of a well-formed set Fn = {f1, ..., fn} by a field d on the inteval [Inf, Sup] is a well-formed set Fopm. The set has to be calculated in the following way:

if d.le=d.ri:
if d.pl=0: Fopm = S ( Pd0 ( Fn, d ), Inf, Sup) (production quantity=0)
if d.pl>0: Fopm = S ( Pdl ( Fn, d ), Inf, Sup) (production quantity>0)
if d.le<d.ri:
if d.pl=0:F*n = P* ( Fn, d) (for * = d0, dr, fl, fr)
Fopm = CC (S (RR (RR ( Fd0n, Ffln ), LL ( Fdrn, Ffrn ) ), Inf, Sup) )
if d.pl>0:F*n = P* ( Fn, d) (for * = dl, dr, fl, fr)
Fopm = CC (S (RR (RR ( Fdln, Ffln ), LL ( Fdrn, Ffrn ) ), Inf, Sup) )
In general:
Fopm = op (Fn, d, Inf, Sup) = {fop1, ..., fopm}
Meaning:
If Fn is the representation of an optimum total cost function in a certain period, d is the representation of the appropriate production cost function in the next period and [Inf, Sup] is feasible inventory interval in the next period then the resulting field-set is the representation of an optimum total cost function without holding costs in the next period. The appropriate model has no start-up costs (o), linear production costs + set-up costs (p) and no holding costs, resulting in the notation op.
3. 8. 2 Optimum-Transformation opt of a well-formed set Fn by a field d and a field g

The result of an Optimum-Transformation opt of a well-formed set Fn = {f1, ..., fn} by a field d and a field g is a well-formed set Foptm. The set has to be calculated by:
Foptm = H ( op ( Fn, d, g.le, g.ri ), g )
In general:
Foptm = opt (Fn, d, g) = {fopt1, ..., foptm}
Meaning:
If Fn is the representation of an optimum total cost function in a certain period, d is the representation of the appropriate production cost function in the next period and g is the representation of the appropriate holding cost function in the next period in the feasible inventory interval then the resulting field-set is the representation of an optimum total cost function in the next period. The appropriate model has no start-up costs (o), linear production costs + set-up costs (p) and linear holding costs (t), resulting in the notation opt.
3. 8. 3 Optimum-Transformation oPt of a well-formed field-set Fn by a well-formed field-set Dk and a field g

The result of an Optimum-Transformation oPt of a well-formed set Fn = {f1, ..., fn} by a well-formed set Dk = {d1, ..., dk} and a field g is the well-formed set FoPtm. The set has to be calculated recursively by
F1n(1) = op (Fn, d1, g.le, g.ri)
and
Fi+1n(i+1) = CC (RR (Fin(i), op (Fn, di+1, g.le, g.ri) ) ) (for i = 1 ... k-1)
and
FoPtm = H ( Fkn(k) , g )
In general:
FoPtm = oPt (Fn, Dk, g) = {foPt1, ..., foPtm}
Meaning:
If Fn is the representation of an optimum total cost function in a certain period, Dk is the representation of the appropriate production cost function in the next period and g is the representation of the appropriate holding cost function in the next period in the feasible inventory interval then the resulting field-set is the representation of an optimum total cost function in the next period. The appropriate model has no start-up costs (o), piecewise linear production costs + set-up costs (P) and linear holding costs (t), resulting in the notation oPt.
3. 8. 4 Optimum-Transformation opT of a well-formed field-set Fn by a field d and a well-formed field-set Go

The result of an Optimum-Transformation opT of a well-formed set Fn = {f1, ..., fn} by a field d and a well-formed set Go = {g1, ..., go} is the well-formed set FopTm. The set has to be calculated by
F1n(1) = op (Fn, d, g1.le, go.ri)
and
FopTm = CC (HH (F1n(1), Go))
In general:
FopTm = opT (Fn, d, Go) = {fopT1, ..., fopTm}
Meaning:
If Fn is the representation of an optimum total cost function in a certain period, d is the representation of the appropriate production cost function in the next period and Go is the representation of the appropriate holding cost function in the next period in the feasible inventory interval then the resulting field-set is the representation of an optimum total cost function in the next period. The appropriate model has no start-up costs (o), linear production costs + set-up costs (p) and piecewise linear holding costs (T), resulting in the notation opT.
3. 8. 5 Optimum-Transformation oPT of a well-formed field-set Fn by a well-formed field-set Dk and a well-formed field-set Go

The result of an Optimum-Transformation oPT of a well-formed set Fn = {f1, ..., fn} by a well-formed set Dk = {d1, ..., dk} and a well-formed set Go = {g1, ..., go} is the well-formed set FoPTm. The set has to be calculated recursively by
F1n(1) = op (Fn, d1, g.le, g.ri)
and
Fi+1n(i+1) = CC (RR (Fin(i), op (Fn, di+1, g.le, g.ri) ) ) (for i = 1 ... k-1)
and
FoPTm = CC (HH (Fkn(k), Go))
In general:
FoPTm = oPT (Fn, Dk, Go) = {foPT1, ..., foPTm}
Meaning:
If Fn is the representation of an optimum total cost function in a certain period, Dk is the representation of the appropriate production cost function in the next period and Go is the representation of the appropriate holding cost function in the next period in the feasible inventory interval then the resulting field-set is the representation of an optimum total cost function in the next period. The appropriate model has no start-up costs (o), piecewise linear production costs + set-up costs (P) and piecewise linear holding costs (T), resulting in the notation oPT.
3. 8. 6 Optimum-Transformation Opt of two well-formed sets Em and Fn by an integer c, a field d and a field g

The result of the Optimum-Transformations OptE and OptF of two well-formed sets Em = {e1, ..., em} and Fn ={f1, ..., fn} by an integer c, a field d and a field g is a well-formed set EOptp and a well-formed set FOptq , respectively. The sets have to be calculated by:

if d.pl=0:
EOptp = H (CC (S (MM (Pd0 (Fn, d), Pd0 (Em, d)), g.le, g.ri)), g)
if d.pl>0:
EOptp = {}
In general:
EOptp = OptE (Em, Fn, d, g) = {eOpt1, ..., eOptp}
d.pl = 1
Foptn(1) = opt (Fn, d, g)
d.hl = d.hl + c
FOptq = CC (MM (Foptn(1), opt (Em, d, g)))
In general:
FOptq = OptF (Em, Fn, c, d, g) = {fOpt1, ..., fOptq}
Meaning:
If Em is the representation of an optimum total cost function in a certain period with production quantity=0 and no set-up costs, Fn is the representation with any production quantity and set-up costs, c is the amount of the start-up costs in the next period, d is the representation of the appropriate production cost function in the next period with no start-up costs and g is the representation of the appropriate holding cost function in the next period in the feasible inventory interval then the resulting field-sets are the representation of an optimum total cost function in the next period. The appropriate model has start-up costs (O), linear production costs + set-up costs (p) and linear holding costs (t), resulting in the notation Opt.
3. 8. 7 Optimum-Transformation OPt of two well-formed sets Em and Fn by an integer c, a well-formed field-set Dk and a field g

The result of the Optimum-Transformations OPtE and OPtF of two well-formed sets Em = {e1, ..., em} and Fn ={f1, ..., fn} by an integer c, a well-formed field-set Dk ={d1, ..., dk} and a field g is a well-formed set EOPtp and a well-formed set FOPtq , respectively. The sets have to be calculated by:

if d1.pl=0:
EOPtp = H (CC (S (MM (Pd0 (Fn, d1), Pd0 (Em, d1)), g.le, g.ri)), g)
if d1.pl>0:
EOPtp = {}
In general:
EOPtp = OPtE (Em, Fn, Dk, g) = {eOPt1, ..., eOPtp}
d1.pl = 1
F1n(1) = op (Fn, d1, g.le, g.ri)
Fi+1n(i+1) = CC (RR (Fin(i), op (Fn, di+1, g.le, g.ri) ) ) (for i = 1 ... k-1)
di.hl = di.hl + c (for i = 1 ... k)
E1m(1) = op (Em, d1, g.le, g.ri)
Ei+1m(i+1) = CC (RR (Eim(i), op (Em, di+1, g.le, g.ri) ) ) (for i = 1 ... k-1)
FOPtq = H (CC (MM (Fkn(k), Ekm(k)) ), g)
In general:
FOPtq = OPtF (Em, Fn, c, Dk, g) = {fOPt1, ..., fOPtq}
Meaning:
If Em is the representation of an optimum total cost function in a certain period with production quantity=0 and no set-up costs, Fn is the representation with any production quantity and set-up costs, c is the amount of the start-up costs in the next period, Dk is the representation of the appropriate production cost function in the next period with no start-up costs and g is the representation of the appropriate holding cost function in the next period in the feasible inventory interval then the resulting field-sets are the representation of an optimum total cost function in the next period. The appropriate model has start-up costs (O), piecewise linear production costs + set-up costs (P) and linear holding costs (t), resulting in the notation OPt.
3. 8. 8 Optimum-Transformation OpT of two well-formed sets Em and Fn by an integer c, a field d and a well-formed field-set Go

The result of the Optimum-Transformations OpTE and OpTF of two well-formed sets Em = {e1, ..., em} and Fn ={f1, ..., fn} by an integer c, a field d and a well-formed field-set Go ={g1, ..., go} is a well-formed set EOpTp and a well-formed set FOpTq , respectively. The sets have to be calculated by:

if d.pl=0:
E1m(1) = CC (S (MM (Pd0 (Fn, d), Pd0 (Em, d)), g1.le, go.ri))
EOpTp = CC ( HH (E1m(1), Go))
if d.pl>0:
EOpTp = {}
In general:
EOpTp = OpTE (Em, Fn, d, Go) = {eOpT1, ..., eOpTp}
d.pl = 1
FopTn(1) = opT (Fn, d, Go)
d.hl = d.hl + c
FOpTq = CC (MM (FopTn(1), opT (Em, d, Go)))
In general:
FOpTq = OpTF (Em, Fn, c, d, Go) = {fOpT1, ..., fOpTq}
Meaning:
If Em is the representation of an optimum total cost function in a certain period with production quantity=0 and no set-up costs, Fn is the representation with any production quantity and set-up costs, c is the amount of the start-up costs in the next period, d is the representation of the appropriate production cost function in the next period with no start-up costs and Go is the representation of the appropriate holding cost function in the next period in the feasible inventory interval then the resulting field-sets are the representation of an optimum total cost function in the next period. The appropriate model has start-up costs (O), linear production costs + set-up costs (p) and piecewise linear holding costs (T), resulting in the notation OpT.
3. 8. 9 Optimum-Transformation OPT of two well-formed sets Em and Fn by an integer c, a well-formed field-set Dk and a well-formed field-set Go

The result of the Optimum-Transformations OPTE and OPTF of two well-formed sets Em = {e1, ..., em} and Fn ={f1, ..., fn} by an integer c, a well-formed field-set Dk ={d1, ..., dk} and a well-formed field-set Go ={g1, ..., go} is a well-formed set EOPTp and a well-formed set FOPTq , respectively. The sets have to be calculated by:

if d1.pl=0:
E1m(1) = CC (S (MM (Pd0 (Fn, d1), Pd0 (Em, d1)), g1.le, go.ri))
EOPTp = CC ( HH (E1m(1), Go))
if d1.pl>0:
EOPTp = {}
In general:
EOPTp = OPTE (Em, Fn, Dk, Go) = {eOPT1, ..., eOPTp}
d1.pl = 1
F1n(1) = op (Fn, d1, g1.le, go.ri)
Fi+1n(i+1) = CC (RR (Fin(i), op (Fn, di+1, g1.le, go.ri) ) ) (for i = 1 ... k-1)
di.hl = di.hl + c (for i = 1 ... k)
E1m(1) = op (Em, d1, g1.le, go.ri)
Ei+1m(i+1) = CC (RR (Eim(i), op (Em, di+1, g1.le, go.ri) ) ) (for i = 1 ... k-1)
FOPTq = CC (HH (MM (Fkn(k), Ekm(k)), G) )
In general:
FOPTq = OPTF (Em, Fn, c, Dk, Go) = {fOPT1, ..., fOPTq}
Meaning:
If Em is the representation of an optimum total cost function in a certain period with production quantity=0 and no set-up costs, Fn is the representation with any production quantity and set-up costs, c is the amount of the start-up costs in the next period, Dk is the representation of the appropriate production cost function in the next period with no start-up costs and Go is the representation of the appropriate holding cost function in the next period in the feasible inventory interval then the resulting field-sets are the representation of an optimum total cost function in the next period. The appropriate model has start-up costs (O), piecewise linear production costs + set-up costs (P) and piecewise linear holding costs (T), resulting in the notation OPT.

4 Definition of the basic operations

4. 1 Production-Transformation

 The Production-Transformations p* (* = d0, dl, dr, fl, fr) of a field f by a field d are defined by:
fd0 = {pl = f.le
pr = f.ri
le = f.le + d.le
ri = f.ri + d.le
hl = f.hl
dh = f.dh }

fdl = {pl = f.le
pr = f.ri
le = f.le + d.le
ri = f.ri + d.le
hl = f.hl + d.hl
dh = f.dh }

fdr = {pl = f.le
pr = f.ri
le = f.le + d.ri
ri = f.ri + d.ri
hl = f.hl + d.hl + (d.ri-d.le)*d.dh
dh = f.dh }

ffl = {pl = f.le
pr = f.le
le = f.le + d.le
ri = f.le + d.ri
hl = f.hl + d.hl
dh = d.dh }

ffr = {pl = f.ri
pr = f.ri
le = f.ri + d.le
ri = f.ri + d.ri
hl = f.hl + (f.ri-f.le)*f.dh + d.hl
dh = d.dh }

F*1 = p*(f, d) = { f*1 } (* = d0, dl, dr, fl, fr)

4. 2 Minimum-Interference

 4. 2. 1 Case-Identification

The following cases can occur by a Minimum-Interference m of a field f with a field d:
( 1, * ):d.le < f.le+1
( 2, * ):f.le < d.le < f.ri+1
( 3, * ):f.ri < d.le
( *, 1 ):d.ri < f.le
( *, 2 ):f.le-1 < d.ri < f.ri
( *, 3 ):f.ri-1 < d.ri
There are 9 combinations, that can be distinguished by identity numbers (Case-Id’s). Cases with f.le>f.ri or d.le>d.ri are impossible.
CaseCase-IdType of result
( 1, 1 ):1 (= 1*1)Fmk = Fm1
( 2, 1 ):0not possible
( 3, 1 ):0not possible
( 1, 2 ):2 (= 1*2)Fmk = Fm1 or Fm2 or Fm3
( 2, 2 ):4 (= 2*2)Fmk = Fm1 or Fm3
( 3, 2 ):0not possible
( 1, 3 ):3 (= 1*3)Fmk = Fm1 or Fm2
( 2, 3 ):6 (= 2*3)Fmk = Fm1 or Fm2 or Fm3
( 3, 3 ):9 (= 3*3)Fmk = Fm1
4. 2. 2 Calculation instruction for Case-Id 1 and Case-Id 9

Case (d.le < f.le+1 and d.ri < f.le) or (f.ri < d.le and f.ri-1 < d.ri):
Fmk = m(f, d) = Fm1 = { fm1 } = { f }
4. 2. 3 Calculation instruction for Case-Id 2

Case d.le < f.le+1 and f.le-1 < d.ri < f.ri:

Calculation of the integer variables dl and dr
dl = f.hl - ( d.hl + ( f.le - d.le ) * d.dh )
dr = ( f.hl + ( d.ri - f.le ) * f.dh ) - ( d.hl + ( d.ri -d.le ) * d.dh )
If ( dl>0 and dr<0 ) or ( dl<0 and dr >0 ) Calculation of the integer variable lr with
lr < ( dl * d.ri - dr * f.le ) / (dl - dr ) < lr + 1 or lr = ( dl * d.ri - dr * f.le ) / (dl - dr )
Sub-Case 2.1: dl-1<0 and dr-1<0
Fmk = m(f, d) = Fm1 = { fm1 } = { f }
Sub-Case 2.2: dl+1>0 and dr+1>0
fm1 = {pl = d.pl + ( f.le - d.le ) * sign ( d.pr - d.pl )
pr = d.pr
le = f.le
ri = d.ri
hl = d.hl + ( f.le - d.le ) * d.dh
dh = d.dh }

fm2 = {pl = f.pl + ( d.ri + 1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = d.ri + 1
ri = f.ri
hl = f.hl + ( d.ri + 1 - f.le ) * f.dh
dh = f.dh }

Fmk = m(f, d) = Fm2 = { fm1, fm2 }
Sub-Case 2.3: dl>0 and dr<0
fm1 = {pl = d.pl + ( f.le - d.le ) * sign ( d.pr - d.pl )
pr = d.pl + ( lr - d.le ) * sign ( d.pr - d.pl )
le = f.le
ri = lr
hl = d.hl + ( f.le - d.le ) * d.dh
dh = d.dh }

fm2 = {pl = f.pl + ( lr + 1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = lr + 1
ri = f.ri
hl = f.hl + ( lr + 1 - f.le ) * f.dh
dh = f.dh }

Fmk = m(f, d) = Fm2 = { fm1, fm2 }
Sub-Case 2.4: dl<0 and dr>0
fm1 = {pl = f.pl
pr = f.pl + ( lr - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = lr
hl = f.hl
dh = f.dh }

fm2 = {pl = d.pl + ( lr + 1 - d.le ) * sign ( d.pr - d.pl )
pr = d.pr
le = lr + 1
ri = d.ri
hl = d.hl + ( lr + 1 - d.le ) * d.dh
dh = d.dh }

fm3 = {pl = f.pl + ( d.ri + 1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = d.ri + 1
ri = f.ri
hl = f.hl + ( d.ri + 1 - f.le ) * f.dh
dh = f.dh }

Fmk = m(f, d) = Fm3 = { fm1, fm2 , fm3 }
4. 2. 4 Calculation instruction for Case-Id 3

Case d.le < f.le+1 and f.ri-1 < d.ri:

Calculation of the integer variables dl and dr
dl = f.hl - ( d.hl + ( f.le - d.le ) * d.dh )
dr = ( f.hl + ( f.ri - f.le ) * f.dh ) - ( d.hl + ( f.ri -d.le ) * d.dh )
If ( dl>0 and dr<0 ) or ( dl<0 and dr >0 ) Calculation of the variable lr with
lr < ( dl * f.ri - dr * f.le ) / (dl - dr ) < lr + 1 or
lr = ( dl * f.ri - dr * f.le ) / (dl - dr )
Sub-Case 3.1: dl-1<0 and dr-1<0
Fmk = m(f, d) = Fm1 = { fm1 } = { f }
Sub-Case 3.2: dl+1>0 and dr+1>0
fm1 = {pl = d.pl + ( f.le - d.le ) * sign ( d.pr - d.pl )
pr = d.pl + ( f.ri - d.le ) * sign ( d.pr - d.pl )
le = f.le
ri = f.ri
hl = d.hl + ( f.le - d.le ) * d.dh
dh = d.dh }

Fmk = m(f, d) = Fm1 = { fm1 }
Sub-Case 3.3: dl>0 and dr<0
fm1 = {pl = d.pl + ( f.le - d.le ) * sign ( d.pr - d.pl )
pr = d.pl + ( lr - d.le ) * sign ( d.pr - d.pl )
le = f.le
ri = lr
hl = d.hl + ( f.le - d.le ) * d.dh
dh = d.dh }

fm2 = {pl = f.pl + ( lr + 1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = lr + 1
ri = f.ri
hl = f.hl + ( lr + 1 - f.le ) * f.dh
dh = f.dh }

Fmk = m(f, d) = Fm2 = { fm1, fm2 }
Sub-Case 3.4: dl<0 and dr>0
fm1 = {pl = f.pl
pr = f.pl + ( lr - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = lr
hl = f.hl
dh = f.dh }

fm2 = {pl = d.pl + ( lr + 1 - d.le ) * sign ( d.pr - d.pl )
pr = d.pl + ( f.ri - d.le ) * sign ( d.pr - d.pl )
le = lr + 1
ri = f.ri
hl = d.hl + ( lr + 1 - d.le ) * d.dh
dh = d.dh }

Fmk = m(f, d) = Fm2 = { fm1, fm2 }
4. 2. 5 Calculation instruction for Case-Id 4

Case f.le < d.le < f.ri+1 and f.le-1 < d.ri < f.ri:

Calculation of the integer variables dl and dr
dl = ( f.hl + ( d.le - f.le ) * f.dh ) - d.hl
dr = ( f.hl + ( d.ri - f.le ) * f.dh ) - ( d.hl + ( d.ri -d.le ) * d.dh )
If ( dl>0 and dr<0 ) or ( dl<0 and dr >0 ) Calculation of the variable lr with
lr < ( dl * d.ri - dr * d.le ) / (dl - dr ) < lr + 1 or
lr = ( dl * d.ri - dr * d.le ) / (dl - dr )
Sub-Case 4.1: dl-1<0 and dr-1<0
Fmk = m(f, d) = Fm1 = { fm1 } = { f }
Sub-Case 4.2: dl+1>0 and dr+1>0
fm1 = {pl = f.pl
pr = f.pl + ( d.le - 1 - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = d.le - 1
hl = f.hl
dh = f.dh }

fm2 = d

fm3 = {pl = f.pl + ( d.ri + 1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = d.ri + 1
ri = f.ri
hl = f.hl + ( d.ri + 1 - f.le ) * f.dh
dh = f.dh }

Fmk = m(f, d) = Fm3 = { fm1, fm2, fm3 }
Sub-Case 4.3: dl>0 and dr<0
fm1 = {pl = f.pl
pr = f.pl + ( d.le - 1 - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = d.le - 1
hl = f.hl
dh = f.dh }

fm2 = {pl = d.pl
pr = d.pl + ( lr - d.le ) * sign ( d.pr - d.pl )
le = d.le
ri = lr
hl = d.hl
dh = d.dh }

fm3 = {pl = f.pl + ( lr + 1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = lr + 1
ri = f.ri
hl = f.hl + ( lr + 1 - f.le ) * f.dh
dh = f.dh }

Fmk = m(f, d) = Fm3 = { fm1, fm2, fm3 }
Sub-Case 4.4: dl<0 and dr>0
fm1 = {pl = f.pl
pr = f.pl + ( lr - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = lr
hl = f.hl
dh = f.dh }

fm2 = {pl = d.pl + ( lr +1 - d.le ) * sign ( d.pr - d.pl )
pr = d.pr
le = lr + 1
ri = d.ri
hl = d.hl + ( lr +1 - d.le ) * d.dh
dh = d.dh }

fm3 = {pl = f.pl + ( d.ri + 1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = d.ri + 1
ri = f.ri
hl = f.hl + ( d.ri + 1 - f.le ) * f.dh
dh = f.dh }

Fmk = m(f, d) = Fm3 = { fm1, fm2, fm3 }
4. 2. 6 Calculation instruction for Case-Id 6

Case f.le < d.le < f.ri+1 and f.ri-1 < d.ri:

Calculation of the integer variables dl and dr
dl = ( f.hl + ( d.le - f.le ) * f.dh ) - d.hl )
dr = ( f.hl + ( f.ri - f.le ) * f.dh ) - ( d.hl + ( f.ri -d.le ) * d.dh )
If ( dl>0 and dr<0 ) or ( dl<0 and dr >0 ) Calculation of the integer variables lr with
lr < ( dl * f.ri - dr * d.le ) / (dl - dr ) < lr + 1 or
lr = ( dl * f.ri - dr * d.le ) / (dl - dr )
Sub-Case 6.1: dl-1<0 and dr-1<0
Fmk = m(f, d) = Fm1 = { fm1 } = { f }
Sub-Case 6.2: dl+1>0 and dr+1>0
fm1 = {pl = f.pl
pr = f.pl + ( d.le - 1 - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = d.le - 1
hl = f.hl
dh = f.dh }

fm2 = {pl = d.pl
pr = d.pl + ( f.ri - d.le ) * sign (d.pr - d.pl )
le = d.le
ri = f.ri
hl = d.hl
dh = d.dh }

Fmk = m(f, d) = Fm2 = { fm1, fm2 }
Sub-Case 6.3: dl>0 and dr<0
fm1 = {pl = f.pl
pr = f.pl + ( d.le - 1 - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = d.le - 1
hl = f.hl
dh = f.dh }

fm2 = {pl = d.pl
pr = d.pl + ( lr - d.le ) * sign ( d.pr - d.pl )
le = d.le
ri = lr
hl = d.hl
dh = d.dh }

fm3 = {pl = f.pl + ( lr + 1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = lr + 1
ri = f.ri
hl = f.hl + ( lr + 1 - f.le ) * f.dh
dh = f.dh }

Fmk = m(f, d) = Fm3 = { fm1, fm2 , fm3 }
Sub-Case 6.4: dl<0 and dr>0
fm1 = {pl = f.pl
pr = f.pl + ( lr - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = lr
hl = f.hl
dh = f.dh }

fm2 = {pl = d.pl + ( lr + 1 - d.le ) * sign ( d.pr - d.pl )
pr = d.pl + ( f.ri - d.le ) * sign ( d.pr - d.pl )
le = lr + 1
ri = f.ri
hl = d.hl + ( lr + 1 - d.le ) * d.dh
dh = d.dh }

Fmk = m(f, d) = Fm2 = { fm1, fm2 }

4. 3 Left-Interference

 The following cases can occur by a Left-Interference l of a field f with a field d:

Case 1: d.le < f.le and f.le < d.ri + 2
fl1 = {pl = d.pl
pr = d.pl + ( f.le -1 - d.le ) * sign ( d.pr - d.pl )
le = d.le
ri = f.le - 1
hl = d.hl
dh = d.dh }

Flk = l(f, d) = { fl1, m(f, d) }
Case else:
Flk = l(f, d) = m(f, d)

4. 4 Right-Interference

 The following cases can occur by a Right-Interference r of a field f with a field d:

Case 1: f.ri < d.ri and d.le < f.ri + 2
frk = {pl = d.pl + ( f.ri + 1 - d.le ) * sign ( d.pr - d.pl )
pr = d.pr
le = f.ri+1
ri = d.ri
hl = d.hl + ( f.ri + 1 - d.le ) * d.dh
dh = d.dh }

Frk = r(f, d) = { m(f, d), frk }
Case else:
Frk = r(f, d) = m(f, d)

4. 5 Section

 4. 5. 1 Case-Identification

The following cases can occur by a Section s of a field f on the interval [Inf, Sup]:
( 1, * ):Inf < f.le+1
( 2, * ):f.le < Inf < f.ri+1
( 3, * ):f.ri < Inf
( *, 1 ):Sup < f.le
( *, 2 ):f.le-1 < Sup < f.ri
( *, 3 ):f.ri-1 < Sup
There are 9 combinations, that can be distinguished by identity numbers (Case-Id’s). Cases with f.le>f.ri or Inf>Sup are impossible.
CaseCase-IdType of result
( 1, 1 ):1 (= 1*1)Fbk = Fb0 = {}
( 2, 1 ):0not possible
( 3, 1 ):0not possible
( 1, 2 ):2 (= 1*2)Fbk = Fb1
( 2, 2 ):4 (= 2*2)Fbk = Fb1
( 3, 2 ):0not possible
( 1, 3 ):3 (= 1*3)Fbk = Fb1 = { fb1 } = { f }
( 2, 3 ):6 (= 2*3)Fbk = Fb1
( 3, 3 ):9 (= 3*3)Fbk = Fb0 = {}
4. 5. 2 Calculation instruction for Case-Id 2

Case Inf < f.le+1 and f.le-1 < Sup < f.ri:
fb1 = {pl = f.pl
pr = f.pl + ( Sup - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = Sup
hl = f.hl
dh = f.dh }

Fbk = b(f, Inf, Sup) = Fb1 = { fb1}
4. 5. 3 Calculation instruction for Case-Id 4

Case f.le<Inf < f.ri+1 and f.le-1 < Sup < f.ri:
fb1 = {pl = f.pl + ( Inf - f.le ) * sign ( f.pr - f.pl )
pr = f.pl + ( Sup - f.le ) * sign ( f.pr - f.pl )
le = Inf
ri = Sup
hl = f.hl + ( Inf - f.le ) * f.dh
dh = f.dh }

Fbk = b(f, Inf, Sup) = Fb1 = { fb1}
4. 5. 4 Calculation instruction for Case-Id 6

Case f.le<Inf < f.ri+1 and f.ri-1 < Sup:
fb1 = {pl = f.pl + ( Inf - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = Inf
ri = f.ri
hl = f.hl + ( Inf - f.le ) * f.dh
dh = f.dh }

Fbk = b(f, Inf, Sup) = Fb1 = { fb1}

4. 6 Consolidation

 The following cases can occur by a Consolidation c of a field f1 with a field f2:

Case 1: f1.ri + 1 = f2.le

Sub-Case1.1: (f1.hl + ( f2.le - f1.le ) * f1.dh = f2.hl and
f1.hl + ( f2.ri - f1.le ) * f1.dh = f2.hl + ( f2.ri - f2.le ) * f2.dh and
f1.pl + ( f2.le - f1.le ) * sign ( f1.pr - f1.pl ) = f2.pl and
f1.pl + ( f2.ri - f1.le ) * sign ( f1.pr - f1.pl ) = f2.pr)
fv1 = {pl = f1.pl
pr = f2.pr
le = f1.le
ri = f2.ri
hl = f1.hl
dh = f1.dh }

Fvk = v (f1, f2) = Fv1 = { fv1 }
Sub-Case1.2: (f2.hl - ( f2.le - f1.le ) * f2.dh = f1.hl and
f2.hl - ( f2.le - f1.ri ) * f2.dh = f1.hl + ( f1.ri - f1.le ) * f1.dh and
f2.pl - ( f2.le - f1.le ) * sign ( f2.pr - f2.pl ) = f1.pl and
f2.pl - ( f2.le - f1.ri ) * sign ( f2.pr - f2.pl ) = f1.pr)
fv1 = {pl = f1.pl
pr = f2.pr
le = f1.le
ri = f2.ri
hl = f1.hl
dh = f2.dh }

Fvk = v (f1, f2) = Fv1 = { fv1 }
Sub-Case 1.else and Case else:
Fvk = v (f1, f2) = Fv2 = { fv1, fv2 } = { f1, f2 }

4. 7 Holding-Transformation

 4. 7. 1 Case-Identification

The following cases can occur by a Holding-Transformation h of a field f by a field g:
( 1, * ):g.le < f.le+1
( 2, * ):f.le < g.le < f.ri+1
( 3, * ):f.ri < g.le
( *, 1 ):g.ri < f.le
( *, 2 ):f.le-1 < g.ri < f.ri
( *, 3 ):f.ri-1 < g.ri
There are 9 combinations, that can be distinguished by identity numbers (Case-Id’s). Cases with f.le>f.ri or g.le>g.ri are impossible.
CaseCase-IdType of result
( 1, 1 ):1 (= 1*1)Fhk = Fh1 = { fh1 } = { f }
( 2, 1 ):0not possible
( 3, 1 ):0not possible
( 1, 2 ):2 (= 1*2)Fhk = Fh2
( 2, 2 ):4 (= 2*2)Fhk = Fb3
( 3, 2 ):0not possible
( 1, 3 ):3 (= 1*3)Fhk = Fh1 = { fh1 }
( 2, 3 ):6 (= 2*3)Fhk = Fh2
( 3, 3 ):9 (= 3*3)Fbk = Fb1 = { fh1 } = { f }
4. 5. 2 Calculation instruction for Case-Id 1 and Case-Id 9

Case (g.le < f.le+1 and g.ri < f.le) or (f.ri < g.le and f.ri-1 < g.ri):
Fhk = h(f, g) = Fh1 = { fh1} = { f }
4. 5. 3 Calculation instruction for Case-Id 2

Case g.le < f.le+1 and f.le-1 < g.ri < f.ri:
fh1 = {pl = f.pl
pr = f.pl + ( g.ri - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = g.ri
hl = f.hl + g.hl + ( f.le - g.le ) * g.dh
dh = f.dh + g.dh}

fh2 = {pl = f.pl + ( g.ri +1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = g.ri+1
ri = f.ri
hl = f.hl + ( g.ri +1 - f.le ) * f.dh
dh = f.dh }

Fhk = h(f, g) = Fh2 = { fh1, fh2}
4. 5. 4 Calculation instruction for Case-Id 3

Case g.le < f.le+1 and f.re-1 < g.ri:
fh1 = {pl = f.pl
pr = f.pr
le = f.le
ri = f.ri
hl = f.hl + g.hl + ( f.le-g.le ) * g.dh
dh = f.dh + g.dh }

Fhk = h(f, g) = Fh1 = { fh1}
4. 5. 5 Calculation instruction for Case-Id 4

Case f.le < g.le < f.ri+1 and f.le-1 < g.re < f.ri:
fh1 = {pl = f.pl
pr = f.pl + ( g.le - 1 - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = g.le - 1
hl = f.hl
dh = f.dh }

fh2 = {pl = f.pl + ( g.le - f.le ) * sign ( f.pr - f.pl )
pr = f.pl + ( g.ri - f.le ) * sign ( f.pr - f.pl )
le = g.le
ri = g.ri
hl = f.hl + ( g.le - f.le ) * f.dh + g.hl
dh = f.dh + g.dh }

fh3 = {pl = f.pl + ( g.ri +1 - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = g.ri+1
ri = f.ri
hl = f.hl + ( g.ri +1 - f.le ) * f.dh
dh = f.dh }

Fhk = h(f, g) = Fh3 = { fh1, fh2, fh3}
4. 5. 6 Calculation instruction for Case-Id 6

Case f.le < g.le < f.ri+1 and f.ri-1 < g.ri:
fh1 = {pl = f.pl
pr = f.pl + ( g.le - 1 - f.le ) * sign ( f.pr - f.pl )
le = f.le
ri = g.le - 1
hl = f.hl
dh = f.dh }

fh2 = {pl = f.pl + ( g.le - f.le ) * sign ( f.pr - f.pl )
pr = f.pr
le = g.le
ri = f.ri
hl = f.hl + ( g.le - f.le ) * f.dh + g.hl
dh = f.dh + g.dh }

Fhk = h(f, g) = Fh2 = { fh1, fh2}

5 Realization of the algorithm to obtain an optimum solution

5. 1 The domain of feasible solutions

 In every period there exists a greatest lower bound (Infimum) and a least upper bound (Supremum) for the inventory quantity (domain of feasible solutions). This can be calculated in the following way:
SetyIInf = Max { yImin; yI }
For i = I-1 down to 1 calculateyiInf = Max { yi+1Inf + di+1 - xi+1max ; yimin }
Sety0Inf = Max { y1Inf + d1 - x1max ; y0 }
For i = 1 up to I calculateyiInf = Max { yi-1Inf + ximin - di ; yiInf }
Sety0Sup = y0
For i = 1 up to I calculateyiSup = Min { yi-1Sup + ximax - di ; yimax }
SetyISup = Min { yISup; yI }
For i = I-1 down to 0 calculateyiSup = Min { yi+1Sup + di+1 - xi+1min; yiSup }
SetIsFeasibleSolution = true
For i = 0 up to I doIf ( yiInf > yiSup ) then IsFeasibleSolution = false
If there exists an i with yiInf > yiSup , then there is no feasible solution. Every feasible solution, especially the wanted optimum solution, must be within the domain of feasible solutions.

5. 2 The algorithm for models with no start-up costs

 The apropriate models have the following properties:
No start-up costs (o), linear production costs + set-up costs (p) or piecewise linear production costs + set-up costs (P), linear holding costs (t) or piecewise linear holding costs (T), resulting in one of the notations opt, oPt, opT or oPT, respectively.

5. 2. 1 Calculation of the domain of feasible solutions
Calculate the domain of feasible solutions using the instruction that is given in chapter 5.1. If there exists no feasible solution then exit.

5. 2. 2 Initializing

Initialize the field-set F01 = {f01} with
f01 = {pl = y0
pr = y0
le = y0
ri = y0
hl = 0
dh = 0 }
5. 2. 3 Calculation of the optimum total cost functions

For i = 1 up to I calculate:

Sub-Step 1:
if (model=opt or model=opT) then calculate field d with
d = {pl = sign(ximin)
pr = 0
le = -di + ximin
ri = Min { ximax - di ; yiSup - yi-1Inf }
hl = si1 + ximin * ci1
dh = ci1 }

if (model=oPt or model=oPT) then calculate field-set DJ(i) = {d1, ..., dJ(i)}with
dj = {pl = sign(xij-1+1)
pr = 0
le = -di + xij-1+1
ri = xij - di
hl = sij + (xij-1 +1) * cij
dh = cij }

if (model=opt or model=oPt) then calculate field g with
g = {pl = 0
pr = 0
le = yimin
ri = yimax
hl = ti1 + yimin * hi1
dh = hi1 }

if (model=opT or model=oPT) then calculate field-set GK(i) = {g1, ..., gK(i)} with
gk = {pl = 0
pr = 0
le = yik-1+1
ri = yik
hl = tik + (yik-1+1)* hik
dh = hik }
Sub-Step 2: Calculate the field-set Fin(i)
if model=opt: Fin(i) = opt ( Fi-1n(i-1), d, g )
if model=oPt: Fin(i) = oPt ( Fi-1n(i-1), DJ(i), g )
if model=opT: Fin(i) = opT ( Fi-1n(i-1), d, GK(i) )
if model=oPT: Fin(i) = oPT ( Fi-1n(i-1), DJ(i), GK(i) )
5. 2. 4 Calculation of the optimum production and inventory quantities

Calculate the optimum inventory quantities in the following way:

For i = I down to 2 calculate:

Sub-Step 1:
Find fi* in Fin(i) = {fi1, ..., fi*, ..., fin(i)}, so that
fi*.le-1 < yi < fi*.ri+1
Sub-Step 2:
Calculate yi-1 = fi*.pl + ( yi - fi*.le ) * sign ( fi*.pr - fi*.pl )
Calculate the optimum production quantities and start-ups in the following way:

For i = 1 up to I calculate:
xi = di + yi - yi-1
ui = sign( xi )

5. 3 The algorithm for models with start-up costs

 The apropriate models have the following properties:
Start-up costs (O), linear production costs + set-up costs (p) or piecewise linear production costs + set-up costs (P), linear holding costs (t) or piecewise linear holding costs (T), resulting in one of the notations Opt, OPt, OpT or OPT, respectively.

5. 3. 1 Calculation of the domain of feasible solutions

Calculate the domain of feasible solutions using the instruction that is given in chapter 5.1. If there exists no feasible solution then exit.

5. 3. 2 Initializing

If u0=1 then initialize the set E00 = { }, if u0=0 then initialize the set E01 = {e01} with
e01 = {pl = y0
pr = y0
le = y0
ri = y0
hl = 0
dh = 0 }
Initialize the set F01 = {f01} with
f01 = {pl = y0
pr = y0
le = y0
ri = y0
hl = ( 1 - u0 ) * a1
dh = 0 }
5. 3. 3 Calculation of the optimum total cost functions

For i = 1 up to I calculate:

Sub-Step 0:
Set the integer c = ai
Sub-Step 1:
if (model=Opt or model=OpT) then calculate field d with
d = {pl = sign(ximin)
pr = 0
le = -di + ximin
ri = Min { ximax - di ; yiSup - yi-1Inf }
hl = si1 + ximin * ci1
dh = ci1 }

if (model=OPt or model=OPT) then calculate field-set DJ(i) = {d1, ..., dJ(i)}with
dj = {pl = sign(xij-1+1)
pr = 0
le = -di + xij-1+1
ri = xij - di
hl = sij + (xij-1 +1) * cij
dh = cij }

if (model=Opt or model=OPt) then calculate field g with
g = {pl = 0
pr = 0
le = yimin
ri = yimax
hl = ti1 + yimin * hi1
dh = hi1 }

if (model=OpT or model=OPT) then calculate field-set GK(i) = {g1, ..., gK(i)}with
gk = {pl = 0
pr = 0
le = yik-1+1
ri = yik
hl = tik + (yik-1+1)* hik
dh = hik }
Sub-Step 2: Calculate the field-sets Eim(i) and Fin(i)
if model=Opt:Eim(i) = OptE (Ei-1m(i-1), Fi-1n(i-1), d, g )
Fin(i) = OptF (Ei-1m(i-1), Fi-1n(i-1), c, d, g )
if model=OPt:Eim(i) = OPtE (Ei-1m(i-1), Fi-1n(i-1), DJ(i), g )
Fin(i) = OPtF (Ei-1m(i-1), Fi-1n(i-1), c, DJ(i), g )
if model=OpT:Eim(i) = OpTE (Ei-1m(i-1), Fi-1n(i-1), d, GK(i) )
Fin(i) = OpTF (Ei-1m(i-1), Fi-1n(i-1), c, d, GK(i) )
if model=OPT:Eim(i) = OPTE (Ei-1m(i-1), Fi-1n(i-1), DJ(i), GK(i) )
Fin(i) = OPTF (Ei-1m(i-1), Fi-1n(i-1), c, DJ(i), GK(i) )
5. 3. 4 Calculation of the optimum production and inventory quantities

Calculate the optimum inventory quantities and start-ups in the following way:
Set a = 0
For i = I down to 1 calculate:
Find fi* in Fin(i) = {fi1, ..., fi*, ..., fin(i)}, so that
fi*.le-1 < yi < fi*.ri+1

Try to find ei* in Eim(i) = {ei1, ..., ei*, ..., ein(i)}, so that
ei*.le-1 < yi < ei*.ri+1

Set c = 1

If there is an ei* then calculate
c = a + (ei*.hl + (yi - ei*.le) * ei*.dh) - (fi*.hl + (yi - fi*.le) * fi*.dh)

If c<0 then calculate
yi-1 = ei*.pl + ( yi - ei*.le ) * sign ( ei*.pr - ei*.pl )
ui = 0

Else calculate
yi-1 = fi*.pl + ( yi - fi*.le ) * sign ( fi*.pr - fi*.pl )
ui = 1

Set a = ai * ui
Calculate the optimum production quantities in the following way:

For i = I downto 1 calculate:
xi = di + yi - yi-1

6 Appendix

6. 1 Graphical representation of the algorithm
This picture shows 5 field-sets which represent the total cost functions for period 1 up to period 5 (P = period, K = total cost, M = inventory quantity).
The red lines (drawn by hand) describe the path of optimum inventory quantities.

6. 2 Computational results

 The algorithm was tested in standard mode = time saving mode and in advanced mode = memory saving mode. The algorithm in time saving mode solves the whole problem at once, that means the algorithm needs memory for I field-sets. The algorithm in memory saving mode solves the problem by solving of sub-problems with I_sub periods, that means the algorithm needs only memory for I_sub field-sets at the same time. The size of sub-problems can be calculated by

I_sub = I / ( ( I + I_sub_max + 1 ) / I_sub_max )

where I_sub_max is the maximum size of a sub-problem that the algorithm should use. The optimum value of I_sub_max depends on the hardware, that means the available RAM. The following data were obtained with I_sub=19 on a PC Pentium with 100 MHz and 8 MB RAM, the code was compiled by the compiler of Borland Turbo C++ 1.0 (c) 1990.

Model opt:
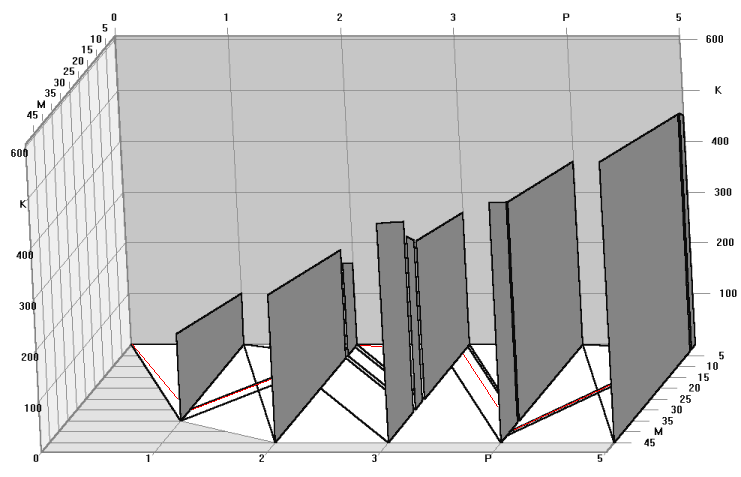
Problem
Size I		Time [sec] using sub-problems of
Size ISize I_sub
730.050.12
1460.100.38
2190.150.83
This shows that there are problem instances which can be solved by the algorithm with linear time in minimum time mode. By using memory saving mode the algorithm works with Time ~ Size ^ 1.75 for this problem instance which increases the time at most by a factor 5.5 for 219 periods.

Model OPT:
Problem
Size I		Time [sec] using sub-problems of
Size ISize I_sub
100.060.06
200.40.5
301.41.7
4045
50912
601622
70out of memory39
80out of memory64
90out of memory98
100out of memory131
Problem
Size I		Time [sec] using sub-problems of
Size ISize I_sub
110out of memory178
120out of memory232
130out of memory294
140out of memory365
150out of memory444
160out of memory504
170out of memory594
180out of memory687
190out of memory789
200out of memory908
Instances that use all features of the algorithm need more time and memory. The algorithm works for this problem instance with Time ~ Size ^ 3.1 in minimum time mode and with Time ~ Size ^ 3.3 in memory saving mode, respectively. The memory saving mode is not too much time consuming in comparison with the minimum time mode, but there is a higher limit for the problem size that can be solved in memory saving mode, so it is recomended to use the algorithm always in memory saving mode.