LT-JobShop

Problembeschreibung:

Mehrere Aufträge (Jobs) sollen mehrere Bearbeitungsstationen durchlaufen, wobei die Reihenfolge für alle Aufträge unterschiedlich sein kann. Dabei können auch Stationen von einzelnen Aufträgen mehrfach oder überhaupt nicht durchlaufen werden. Gesucht ist die Reihenfolge der Aufträge auf den Stationen, bei der die Gesamtdurchlaufzeit oder die maximale Terminüberschreitung minimal wird.

Beispiel:

Ein klassisches und das in der Literatur wohl am häufigsten zitierte Beispiel ist das 10x10-Problem von Muth und Thompson aus dem Jahr 1963, für das erst 1986 die Optimalität einer Lösung, bei der die Gesamtdauer 930 ZE beträgt, bewiesen werden konnte. Das Problem ist durch nachfolgende Daten gegeben:

{ 10 } Aufträge
{ 10 } Operationen je Auftrag
{ 10 } Stationen
Stationsstartzeiten:
{
0 0 0 0 0 0 0 0 0 0
}
Matrix (Stations-Nr. Operationszeit)
{
0 29 1 78 2 9 3 36 4 49 5 11 6 62 7 56 8 44 9 21
0 43 2 90 4 75 9 11 3 69 1 28 6 46 5 46 7 72 8 30
1 91 0 85 3 39 2 74 8 90 5 10 7 12 6 89 9 45 4 33
1 81 2 95 0 71 4 99 6 9 8 52 7 85 3 98 9 22 5 43
2 14 0 6 1 22 5 61 3 26 4 69 8 21 7 49 9 72 6 53
2 84 1 2 5 52 3 95 8 48 9 72 0 47 6 65 4 6 7 25
1 46 0 37 3 61 2 13 6 32 5 21 9 32 8 89 7 30 4 55
2 31 0 86 1 46 5 74 4 32 6 88 8 19 9 48 7 36 3 79
0 76 1 69 3 76 5 51 2 85 9 11 6 40 7 89 4 26 8 74
1 85 0 13 2 61 6 7 8 64 9 76 5 47 3 52 4 90 7 45
}
Auftragstermine:
{
1000 1000 1000 1000 1000 1000 1000 1000 1000 1000
}

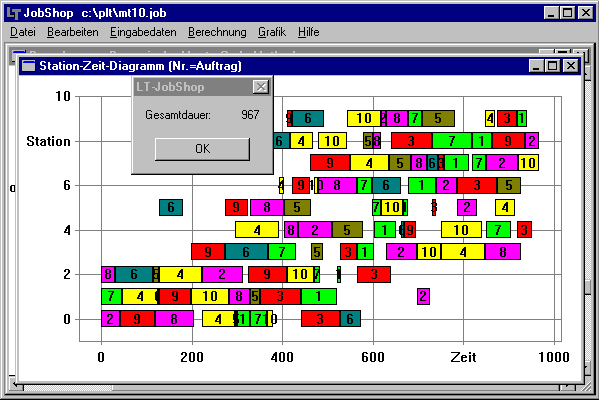
Lösung mittels Programm:

Die obigen Daten innerhalb der geschweiften Klammern können direkt vom Programm als Eingabedaten verarbeitet werden. Mit einem der Lösungsverfahren unter dem Menü "Berechnung" kann eine zulässige Lösung ermittelt und tabellarisch in einem Textfenster sowie graphisch als Gantt-Diagramm dargestellt werden.