Problembeschreibung:
Beim dynamischen Lagerhaltungsmodell für ein Lagergut wird davon ausgegangen, daß über
einen Planungszeitraum von mehreren Perioden die Mengen festzulegen sind, welche von dem
Gut in jeder Periode zu beschaffen sind, so daß die Gesamtkosten minimal werden. Die
Bedarfsmengen, Beschaffungskosten sowie die Lagerkosten je Mengeneinheit müssen bekannt
sein und können für die einzelnen Perioden unterschiedlich sein. Die Beschaffungskosten
setzen sich aus einem fixen und einem (mengenproportionalen) variablen Anteil zusammen.
Die Lagerkosten werden als mengenproportional zum Lagerbestand am Ende einer Periode
angenommen. Das Modell eignet sich beim Fremdbezug von Gütern (Beschaffung=Bestellung) ebenso
wie bei der Eigenfertigung (Beschaffung=Produktion).
Zusätzlich läßt sich das Modell durch eine (periodenabhängige) Beschränkung der Beschaffungs-
und Lagerkapazitäten erweitern.
Beispiel:
Das Beispiel ist sinngemäß entnommen aus: Klaus Neumann (1996), Produktions- und Operations-
Management, Springer, Berlin.
Die prognostizierte Nachfrage nach einem Bauteil und die entsprechende Produktionskapazität
(in ME) sei für 6 aufeinander folgende Monate (Perioden) in nachfolgender Tabelle gegeben:
| Periode | 1 | 2 | 3 | 4 | 5 | 6 |
| Kapazität | 20 | 10 | 20 | 20 | 10 | 10 |
| Bedarf | 5 | 15 | 10 | 5 | 5 | 30 |
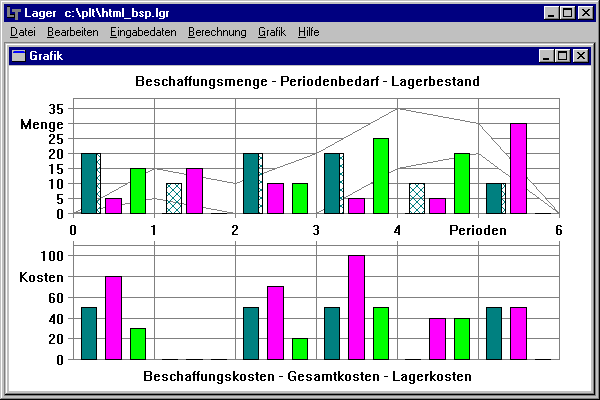
Lösung mittels Programm:
Mit Hilfe des Programms kann eine optimale Lösung für das Problems berechnet und und tabellarisch sowie grafisch dargestellt werden. Bei der optimalen Lösung entstehen Gesamtkosten von 340 DM (nicht-optimierte Lösung: 380 DM).

zur vorigen Seite: Kalender
zur nächsten Seite: Layout
zurück zur Hauptseite
Lutz Tautenhahn, 8/98