LT-Layout

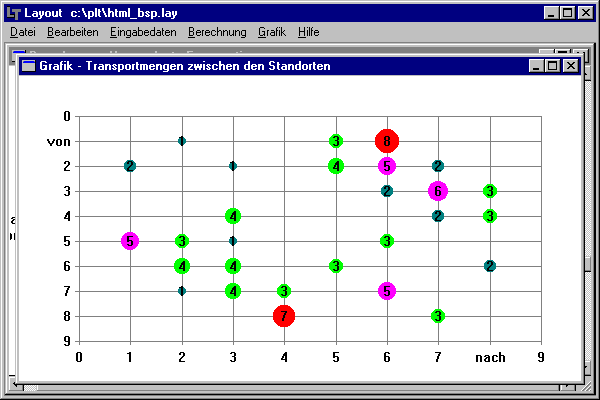
Problembeschreibung:
Beim Layout-Problem (auch innerbetriebliches Standortproblem genannt) sind Anordnungsobjekte so zu potentiellen Standorten zuzuordnen, daß die Gesamttransportleistung möglichst minimal wird. Die Gesamttransportleistung ergibt sich aus dem Produkt aus der Entfernung zwischen zwei Anordnngsobjekten und der zwischen ihnen zu transportierenden Menge, summiert über alle Anordnungsobjekte. Es wird dabei angenommen, daß die Kosten proportional zur Entfernung und Menge sind. Die Anzahl der Anordnungsobjekte ist gleich der Anzahl der potentiellen Standorte, andernfalls werden zusätzlich fiktive Anordnungsobjekte mit Transportmengen gleich Null eingeführt.

Beispiel:

In einer neuerrichteten Maschinenhalle sollen 8 Maschinen in 2 Reihen zu je 4 Maschinen aufgestellt werden. Beim späteren Produktionsprozeß erfolgt der An- und Abtransport der Werkstücke in die Halle und aus der Halle per Gabelstapler, der Transport zwischen den Maschinen per Hubwagen. Die Maschinen sind so aufzustellen, daß die mittels Hubwagen zu erbringende Transportleistung minimal wird.
Skizze (potentielle Standorte):

----------------- | 1 | 2 | 3 | 4 | Nr.=Standort | = = = = = = = <-Ein- und | 5 | 6 | 7 | 8 | Ausgang -----------------

Es gelten die folgenden Daten:
{ 8 } Standorte
Entfernungen zwischen den Standorten (Manhattan-Norm):
v\n 1 2 3 4 5 6 7 8
1 { 0 2 3 4 1 2 3 4 }
2 { 2 0 2 3 2 1 2 3 }
3 { 3 2 0 2 3 2 1 2 }
4 { 4 3 2 0 4 3 2 1 }
5 { 1 2 3 4 0 2 3 4 }
6 { 2 1 2 3 2 0 2 3 }
7 { 3 2 1 2 3 2 0 2 }
8 { 4 3 2 1 4 3 2 0 }
Transportmengen zwischen den Maschinen:
v\n 1 2 3 4 5 6 7 8
1 { 0 3 0 0 6 0 0 2 }
2 { 0 0 7 0 3 0 0 0 }
3 { 4 3 0 0 2 0 0 0 }
4 { 1 0 0 0 2 4 2 5 }
5 { 4 0 3 1 0 0 0 5 }
6 { 1 0 0 3 0 0 5 3 }
7 { 0 0 0 1 0 3 0 8 }
8 { 4 2 0 4 0 3 0 0 }

Lösung mittels Programm:

Die obigen Daten innerhalb der geschweiften Klammern können direkt vom Programm als Eingabedaten verarbeitet werden. Als Lösungsverfahren wurde mittels Vollenumeration (Rechenzeit 20 sec) eine optimale Lösung ermittelt. Die Maschinen sind danach wie folgt anzuordnen (spiegelbildliche Anordnungen sind ebenfalls optimal):

----------------- | 7 | 4 | 1 | 3 | Nr.=Maschine | = = = = = = = <-Ein- und | 6 | 8 | 5 | 2 | Ausgang -----------------

Bei dieser Lösung erhält man für die Gesamttransportleistung einen Wert von 154, bei der Zuordnung Maschine-Standort nach gleicher Nummer beträgt die Transportleistung 223. Der Transportaufwand wird somit durch die Optimierung um ca. ein drittel reduziert.

zur vorigen Seite: Lager
zur nächsten Seite: LosSplit
zurück zur Hauptseite

Lutz Tautenhahn, 8/98