Problembeschreibung:
Beim klassischen Transportproblem geht es darum, Transportmengen zwischen mehreren Orten,
in denen jeweils ein Bedarf oder ein Aufkommen eines einheitlichen Transportgutes besteht,
so festzulegen, daß alle Bedarfe gedeckt werden und die Gesamttransportkosten dabei
minimal werden.
Ausgehend von Orten, die ein Aufkommen besitzen, erfolgt die Belieferung. In den Orte,
in denen ein Bedarf besteht, erfolgt die Abnahme des Transportgutes. Die Transportkosten
werden als proportional zur Menge und Entfernung angenommen.
Die Summe der Bedarfe muß gleich der Summe der Aufkommen sein (geschlossenes Transportproblem).
Wenn das nicht der Fall ist (offenes Transportproblem), so ist ein zusätzlicher fiktiver Ort
mit dem fehlenden Bedarf oder Aufkommen einzuführen, bei dem die Entfernungen zu allen anderen
Orten zu Null gesetzt werden. Dadurch erhält man wieder ein geschlossenes Transportproblem.
Das Zuordnungsproblem kann als ein Spezialfall des Transportproblems gesehen werden. Die Anzahl
der Orte mit Bedarfen ist gleich der Anzahl der Orte mit Aufkommen. Die Bedarfe und Aufkommen
(und damit auch die Transportmengen) betragen jeweils eine Mengeneinheit. Dieser Problemtyp läßt
sich allgemein auch auf viele Bereiche anwenden, bei es nicht um den Transport eines Gutes geht.
Das Rundreiseproblem ist ein Zuordnungsproblem mit einer zusätzlichen Nebenbedingung: Die
Eins-Elemente in der Zuordnungsmatrix müssen einen geschlossenen Kreis ergeben. Es ist also
eine Rundreise gesucht, die durch alle Orte geht, so daß dabei die Gesamtweglänge minimal wird.
Dieser Problemtyp läßt sich auch in anderen Bereichen (z.B. Maschinenbelegungsplanung bei
reihenfolgeabhängigen Rüstzeiten) anwenden.
Beispiel zum Transportproblem:
{ 4 } Baustellen beziehen Sand aus { 3 } Sandgruben. Die Bedarfe der Baustellen betragen dabei
im betrachteten Zeitraum { 24, 12, 10 } und { 8 } Lkw-Ladungen, die Aufkommen der Sandgruben
{ 20, 18 } und { 16 } Lkw-Ladungen. Die Entfernungen zwischen den Baustellen und den
Sandgruben betragen (in km):
¤ BAUSTELLE
S ¤ ¤ 1 2 3 4
A 1 { 8 4 3 9 }
N 2 { 5 7 2 4 }
D 3 { 1 9 5 3 }
Wieviele Lkw-Ladungen an Sand müssen die Baustellen jeweils aus welcher Sandgrube beziehen,
damit der Gesamttransportaufwand minimal wird?
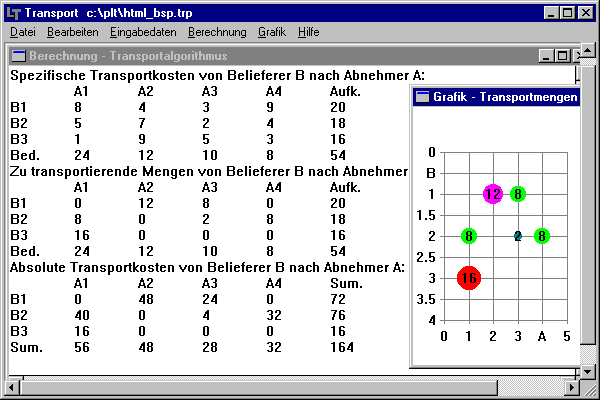
Lösung mittels Programm:
Die obigen Daten innerhalb der geschweiften Klammern können direkt aus dem Fließtext heraus
(bei richtiger Einstellung des Eingabeformates) vom Programm verarbeitet werden.
Mit einem der Lösungsverfahren unter dem Menü "Berechnung" wird eine zulässige Ausgangs-Lösung
ermittelt, aus der nachfolgend die optimale Lösung gewonnen werden kann. Die Lösung wird
tabellarisch in einem Textfenster ausgegeben. Zusätzlich kann eine Grafik dargestellt werden.

Bei der optimalen Lösung dieses Problems beträgt der Gesamttransportaufwand 164 Einheiten (Greedy- und Vogel-Heuristik liefern 180 Einheiten).
Beispiel zum Zuordnungsproblem:
Es war einmal ein Kuhhändler, der hatte { 3 } Töchter, die wollte er gern unter die Haube
bringen. Alsbald standen auch schon { 3 } heiratswillige Kandidaten vor seinem Stall.
Der erste verlangte als Mitgift: Für die älteste Tochter { 10 } Kühe, für die mittlere { 5 }
Kühe und für die jüngste { 1 } Kuh. Der zweite verlangte als Mitgift: Für die älteste Tochter
{ 5 } Kühe, für die mittlere { 6 } Kühe und für die jüngste { 7 } Kühe. Kandidat Nummer { 3 }
verlangte { 3 } mal je { 3 } Kühe.
Der Vater überlegte lange bis nachts um halb { 1 },
erhellt durch den Geist seines Kuhhändlerw{ 1 }.
Die { 1 }icht kam bei Anbruch des Sonnensch{ 1 },
wem er mußte geben die Hand seines kl{ 1 }ten Töchterl{ 1 }.
Wie wird der Kuhhandel abgelaufen sein? Wer bekam welche Tochter und um wieviele Kühe wurde der
Kuhhändler erleichtert?
|
; ; ; ; ; ; ; ; ; ; ; ; ; ; (\__/); ; ; ; ; ; ; ; ; ( oo )______; ; ; ; ; ; ;\../ \ \ \ \ ; ; ; ; ; ; ;\________|\; ; ; ; ; ; ; ||; ; ;|| * ; ; ; ; ; ; ^^; ; ;^^ ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; |
Lösung mittels Programm:
Die obigen Daten innerhalb der geschweiften Klammern können direkt aus dem Fließtext heraus
(bei richtiger Einstellung des Eingabeformates) vom Programm verarbeitet werden.
Mittels Ungarischer Methode kann unmittelbar die optimale Lösung gewonnen werden, d. h.:
Kandidat 1 bekam die jüngste Tochter, Kandidat 2 bekam die älteste und Kandidat 3 bekam
die, die noch übrig war. Der Kuhhändler bekam 9 Kühe los und die Töchter bekamen viele Kinder.
Und wenn sie nicht gestorben sind, dann leben sie noch heute.
Beispiel zum Rundreiseproblem:
5 Aufträge sollen nacheinander eine Anlage durchlaufen. Dabei treten in Abhhängigkeit
von der Bearbeitsreihenfolge folgende Umrüstkosten auf (in GE):
| von\nach | 1 | 2 | 3 | 4 | 5 |
| 1 | - | 11 | 14 | 17 | 13 |
| 2 | 15 | - | 18 | 14 | 12 |
| 3 | 13 | 19 | - | 12 | 14 |
| 4 | 14 | 12 | 15 | - | 11 |
| 5 | 16 | 13 | 11 | 14 | - |
Lösung mittels Programm:
Die Rüstkosten können in Matrix-Form als "Eingabedaten" vom Programm verarbeitet werden.
Die Daten sind dabei entsprechend der Zusatzbedingungen noch zu modifizieren.
Mit einem der Lösungsverfahren unter dem Menü "Berechnung" kann eine zulässige Lösung
ermittelt werden. Diese kann als Ausgangspunkt für eines der Verbesserungsverfahren
verwendet werden. Die Lösung wird tabellarisch in einem Textfenster ausgegeben und kann
zusätzlich als Grafik dargestellt werden.
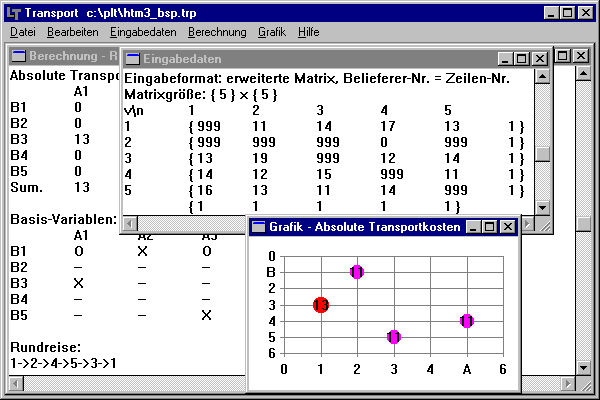
Die vom Programm ermittelte Rundreise 1->2->4->5->3->1(->2->4->5->... ) ergibt die
Auftragsreihenfolge 4->5->3->1->2. Die hier gefundene Lösung ist optimal (Umrüstkosten: 46 GE).
Für große Probleme läßt sich die optimale Lösung kaum noch mit vertretbarer Rechenzeit ermitteln.
Man kann jedoch stets durch die optimale Lösung des äquivalenten Zuordnungsproblems
(Ungarische Methode) zumindest eine untere Schranke für die optimale Lösung des
Rundreiseproblems angeben. (Dabei muß die Hauptdiagonale der Matrix mit hohen Werten
belegt sein, damit dort keine Zuordnungen vorgenommen werden.)
zur vorigen Seite: Statistik
zurück zur Hauptseite
Lutz Tautenhahn, 8/98