Problembeschreibung:
Bei Problemen aus dem Bereich der Statistik geht es darum, aus einer großen Menge verfügbaren
Datenmaterials die interessierenden statistischen Kennzahlen bzw. empirischen Zusammenhänge
zu ermitteln.
So können z.B. aus den bekannten Vergangenheits-Werten und den ermittelten statistischen
Zusammenhängen Prognosen für die zu erwartende zukünftige Entwicklung abgegeben werden
(Zeitreihenanalyse).
Bei stichprobenartig beobachteten Eigenschafts-Kombinationen an mehreren gleichartigen
Objekten können diese quantifiziert werden und somit beim Auftreten einer Eigenschaft auf
die zu erwartende Ausprägung der anderen Eigenschaft(en) geschlußfolgert werden
(Regressionsanalyse).
Beim Vorhandensein großer Datenmengen empfiehlt sich stets eine Klassifizierung, wodurch eine
Überschaubarkeit der Daten erst erreicht wird. Dies findet z.B. Verwendung bei der ABC-Analyse,
bei der Verbrauchsgüter entsprechend ihres Anteils an der Kapitalbindung eingeteilt (und
nachfolgend disponiert) werden.
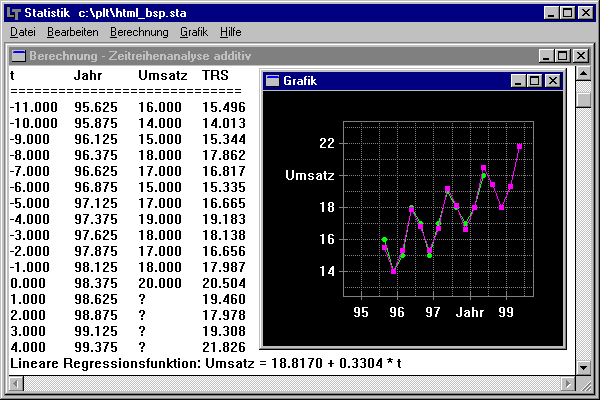
Beispiel zur Zeitreihenanalyse:
Ein Unternehmen plant die zu produzierende Menge eines bestimmten Artikels. Es müsses dafür
rechtzeitig die entsprechenden Mengen an Roh-Material bestellt werden.
In der Vergangenheit konnten folgende Mengen des Artikels verkauft werden:
| Quartal | 3/95 | 4/95 | 1/96 | 2/96 | 3/96 | 4/96 | 1/97 | 2/97 | 3/97 | 4/97 | 1/98 | 2/98 |
| Menge | 16 | 14 | 15 | 18 | 17 | 15 | 17 | 19 | 18 | 17 | 18 | 20 |
Lösung mittels Programm:
Die obigen Daten sind in das Programm einzugeben, anschließend kann vom Programm eine Zeitreihenanalyse durchgeführt und die Werte für die kommenden 4 Quartale ermittelt werden. Die Lösung wird tabellarisch in einem Textfenster ausgegeben und kann zusätzlich grafisch dargestellt werden.

Beispiel zur Regressionsanalyse:
In einem Zoo gibt es 6 Schlangen. Die Längen der einzelnen Schlangen (in Meter) und ihr jeweiliger
Kaninchenbedarf (in Stück pro Monat) sind in folgender Tabelle gegeben:
| Schlangenlänge | 1,20 | 2,10 | 3,00 | 4,40 | 5,20 | 6,40 |
| Kaninchenbedarf | 4 | 6 | 9 | 14 | 18 | 23 |
|
|
Lösung mittels Programm:
Die obigen Daten sind in das Programm einzugeben, anschließend kann vom Programm eine Regressionsanalyse durchgeführt werden. Es wurde in diesem Fall die Berechnung mittels quadratischer Regression durchgeführt. Die Schlange hat demnach pro Monat einen Kaninchenbedarf von voraussichtlich 30 Stück. (Das entspricht in etwa dem Kaloriengehalt einer Tierpflegerin.)

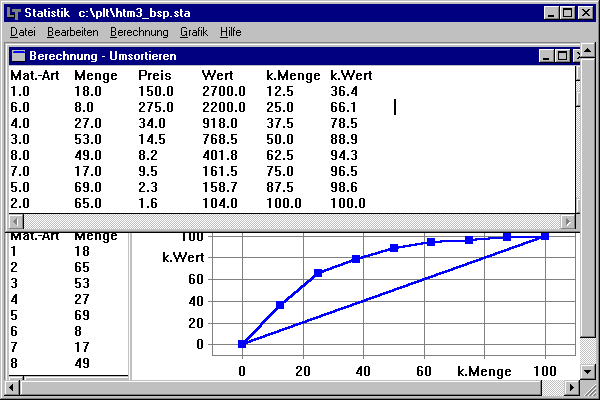
Beispiel zur ABC-Analyse:
Ein Unternehmen hatte im vergangenen Jahr folgende Mengen an Material verbraucht.
Der Verbrauch (in materialspezifischen Mengeneinheiten) sowie die Material-Preise
sind in der folgenden Tabelle gegeben:
| Materialart | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Verbrauch in ME | 18 | 65 | 53 | 27 | 69 | 8 | 17 | 49 |
| Preis in GE/ME | 150 | 1,60 | 14,50 | 34 | 2,30 | 275 | 9,50 | 8,20 |
Lösung mittels Programm:
Die obigen Daten sind in das Programm einzugeben, anschließend wird zunächst eine neue Variable erzeugt: Wert=Menge*Preis. Für diese Variable wird das Konzentrationsmaß bestimmt. Die Ausgabe der Lösung erfolgt tabellatisch in einem Textfenster. Zusätzlich kann eine Grafik dargestellt werden. Die Materialarten 1 und 6 gehören demnach zur Gruppe der A-Güter, die Materialarten 3 und 4 zur Gruppe der B-Güter und die restlichen vier Materialarten zur Gruppe der C-Güter. Die Materialarten sollten dementsprechend disponiert werden.
zur vorherigen Seite: Simplex
zur nächsten Seite: Transport
zurück zur Hauptseite
Lutz Tautenhahn, 8/98