Problembeschreibung:
Eine Lineare Optimierungsaufgabe, d.h. ein System von linearen Gleichungen und Ungleichungen mehrerer (reeller) Variablen und einer zu minimierenden oder zu maximierenden Zielfunktion, kann mittels Simplex-Algorithmus optimal gelöst werden. Damit ist dieses Verfahren zur Lösung aller praktischen Probleme, die sich durch Lineare Optimierungs-Modelle beschreiben lassen, geeignet.
Beispiel:
Ein Kleinunternehmer plant die Herstellung von Erzeugnissen dreier verschiedener Sorten.
Von jeder Sorte müssen mindestens 100 Stück hergestellt werden, maximal können je Sorte
200 Stück hergestellt werden.
Die erwarteten Gewinne betragen 10 DM pro Stück für Sorte 1, 8 DM pro Stück für Sorte 2 und
7 DM pro Stück für Sorte 3. Alle Erzeugnisse müssen auf 3 Maschinen bearbeitet werden,
die im geplanten Zeitraum jeweils 1000 Zeiteinheiten zur Verfügung stehen. Die Bearbeitungsdauer
pro Stück für die Erzeugnisse auf den Maschinen sind in der folgenden Tabelle enthalten:
| Bearb.-Dauer | Erzeugnis 1 | Erzeugnis 2 | Erzeugnis 3 |
| Maschine 1 | 5 | 1 | 1 |
| Maschine 2 | 1 | 3 | 4 |
| Maschine 3 | 2 | 3 | 2 |
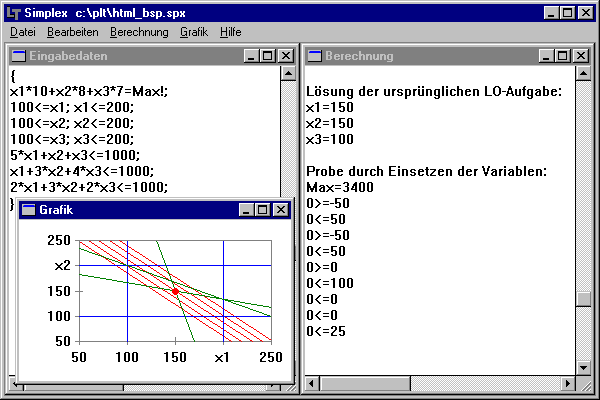
Lösung mittels Programm:
Das obige Problem ist als Lineares Optimierungs-Modell zu formulieren und die entsprechenden Gleichungen und Ungleichungen dazu in das Programm einzugeben. Anschließend kann vom Programm eine optimale Lösung ermittelt sowie grafisch dargestellt werden.

In der Grafik wird die Zielfunktion als Schar von 5 Geraden in roter Farbe dargestellt, wobei
die Lage des Optimums durch einen roten Punkt gekennzeichnet wird.
Gleichungen und Ungleichungen mit einer Variablen werden in blauer Farbe dargestellt,
Gleichungen und Ungleichungen mit mehreren Variablen in grüner Farbe.
Die Zuordnungen der Variablen zu den Achsen sowie der darzustellende Bereich können
geändert werden.
zur vorherigen Seite: OpenShop
zur nächsten Seite: Statistik
zurück zur Hauptseite
Lutz Tautenhahn, 8/98