LT-OpenShop

Problembeschreibung:

Mehrere Aufträge sollen mehrere Bearbeitungsstationen durchlaufen, wobei die Reihenfolge, in welcher ein Auftrag die Stationen durchläuft, beliebig ist. Gesucht ist die Reihenfolge der Aufträge auf den Stationen, bei der die Gesamtdurchlaufzeit oder die maximale Terminüberschreitung minimal wird.

Beispiel:

6 Aufträge (1...6) sollen 4 Bearbeitungsstationen in beliebiger Reihenfolge durchlaufen, so daß die Gesamtbearbeitungsdauer minimal wird und keine Terminüberschreitung auftritt. Die frühesten Bearbeitungsstartzeiten der Stationen, die Bearbeitungsdauern der Aufträge auf den Stationen und die Fertigstellungstermine der Aufträge sind durch die nachfolgenden Daten gegeben:

{ 6 } Aufträge
{ 4 } Bearbeitungsstationen
Bearbeitungsdauern der Aufträge A auf den Stationen B:
B\A 1 2 3 4 5 6
1: { 1 3 5 3 4 2 }
2: { 3 6 4 1 3 2 }
3: { 2 4 5 5 2 3 }
4: { 5 6 4 3 4 1 }
Startzeiten der Stationen:
{ 0 2 5 6 }
Fertigstellungstermine der Aufträge:
{ 33 35 27 30 25 29 }

Lösung mittels Programm:

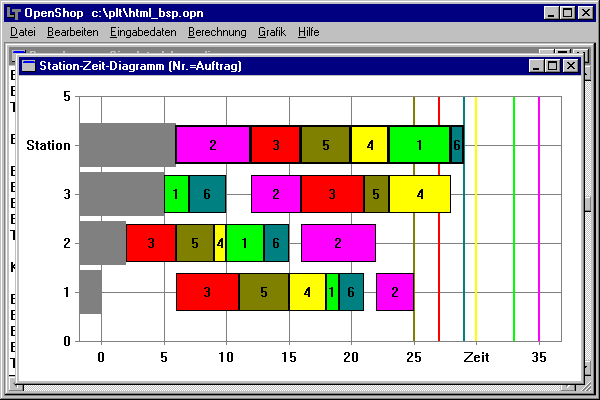
Die obigen Daten innerhalb der geschweiften Klammern können direkt vom Programm als Eingabedaten verarbeitet werden. Mit einem der Lösungsverfahren unter dem Menü "Berechnung" kann eine zulässige Lösung ermittelt und tabellarisch in einem Textfenster sowie graphisch als Gantt-Diagramm dargestellt werden.

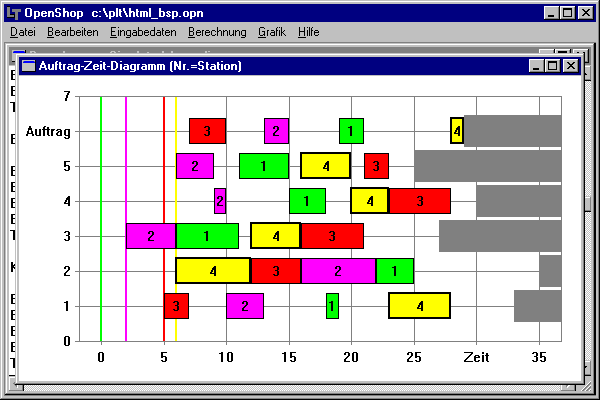
Die beiden Gantt-Diagramme entsprechen dem gleichen Stationsbelegungsplan, im oberen Bild werden die Aufträge im Station-Zeit-Diagramm dargestellt, im unteren Bild die Stationen im Auftrag-Zeit-Diagramm (kritische Vorgänge mit fettem Rand).